题目内容
静止在湖面的小船上有两个人分别向相反方向水平抛出质量相同的小球,甲向左抛,乙向右抛,如图所示。甲先抛,乙后抛,抛出后两小球相对岸的速率相等,若不计水的阻力,则下列说法中正确的是( )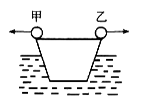
| A.两球抛出后,船往左以一定速度运动,乙球受到的冲量大一些 |
| B.两球抛出后,船往右以一定速度运动,甲球受到的冲量大一些 |
| C.两球抛出后,船的速度为零,甲球受到的冲量大一些 |
| D.两球抛出后,船的速度为零,两球所受的冲量相等 |
C
解析试题分析:设小船的质量为M,小球的质量为m,甲球抛出后,根据动量守恒定律有:mv=(M+m)v′,v′的方向向右.乙球抛出后,规定向右为正方向,根据动量守恒定律有:(M+m)v′=mv+Mv″,解得v″=0.根据动量定理得,所受合力的冲量等于动量的变化,对于甲球,动量的变化量为mv,对于乙球动量的变化量为mv-mv′,知甲的动量变化量大于乙球的动量变化量,所以抛出时,人给甲球的冲量比人给乙球的冲量大.故C正确.
考点:动量守恒定律及动量定理的应用。

从两个等高的平台上,分别以等大的速率抛出两个完全相同的小球,甲球竖直上抛,乙球竖直下抛,若不计空气阻力,则下列表述正确的是
| A.抛出时两球的动量相同 |
| B.落地时两球的动量不同 |
| C.从抛出到落地的过程,两球受到的冲量相同 |
| D.从抛出到落地的过程,两球受到的冲量不同 |
下面关于冲量的说法中正确的是( )
| A.物体受到很大的冲力时,其冲量一定很大 |
| B.当力与位移垂直时,该力的冲量为零 |
| C.不管物体做什么运动,在相同时间内重力的冲量相同 |
| D.只要力的大小恒定,其相同时间内的冲量就恒定 |
如图所示,篮球运动员接传来的篮球时,通常要先伸出两臂迎接,手接触到球后,两臂随球迅速引至胸前,这样做可以
| A.减小球的动量的变化量 |
| B.减小球对手作用力的冲量 |
| C.减小球的动量变化率 |
| D.延长接球过程的时间来减小动量的变化量 |
质量是1 kg的钢球,以5 m/s的速度水平向右运动,碰到墙壁后以3 m/s的速度被反向弹回。假设球与墙面接触的时间是0.1秒,设水平向右为正方向,则( )
| A.钢球的动量变化量为2kg?m/s |
| B.钢球的动量变化量为-2kg?m/s |
| C.墙面对钢球的冲量为8 kg?m/s |
| D.墙面对钢球的冲量为-8 kg?m/s |
在光滑的水平桌面上有等大的质量分别为M="0.6" kg,m="0.2" kg的两个小球,中间夹着一个被压缩的具有Ep="10.8" J弹性势能的轻弹簧(弹簧与两球不相连),原来处于静止状态.现突然释放弹簧,球m脱离弹簧后滑向与水平面相切、半径为R="0.425" m的竖直放置的光滑半圆形轨道,如图所示.g取10 m/s2.则下列说法正确的是:
| A.球m从轨道底端A运动到顶端B的过程中所受合外力冲量大小为3.4 N·s |
| B.M离开轻弹簧时获得的速度为9m/s |
| C.若半圆轨道半径可调,则球m从B点飞出后落在水平桌面上的水平距离随轨道半径的增大而减小 |
| D.弹簧弹开过程,弹力对m的冲量大小为1.8 N·s |
如图所示,小车与木箱紧挨着静放在光滑的水平冰面上,现有一男孩站在小车上用力向右迅速推出木箱,关于上述过程,下列说法中正确的是 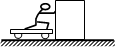
| A.男孩和木箱组成的系统动量守恒 |
| B.小车与木箱组成的系统动量守恒 |
| C.男孩、小车与木箱三者组成的系统动量守恒 |
| D.木箱的动量增量与男孩、小车的总动量增量相同 |