题目内容
【题目】在科学研究中，可以通过施加适当的电场和磁场来实现对带电粒子运动的控制。如图所示，某时刻在xOy平面内的第Ⅱ、Ⅲ象限中施加沿y轴负方向、电场强度为E的匀强电场，在第Ⅰ、Ⅳ象限中施加垂直于xOy坐标平面向里、磁感应强度为B的匀强磁场。一质量为m，电荷量为q的带正电的粒子从M点以速度v0沿垂直于y轴方向射入该匀强电场中，粒子仅在电场力作用下运动到坐标原点O且沿OP方向进入第Ⅳ象限。在粒子到达坐标原点O时撤去匀强电场（不计撤去电场对磁场及带电粒子运动的影响），粒子经过原点O进入匀强磁场中，并仅在磁场力作用下，运动一段时间从y轴上的N点射出磁场。已知OP与x轴正方向夹角α=60°，带电粒子所受重力及空气阻力均可忽略不计，求：
（1）M、O两点间的电势差U；
（2）坐标原点O与N点之间的距离d；
（3）粒子从M点运动到N点的总时间t。
【答案】（1）
（2）
（3）
【解析】试题分析：（1）设粒子经过O点的速度为v， 则cosα=
（1分）
对于电子经过电场的过程，根据动能定理有：
（1分）
解得：
（1分）
（2）设粒子在磁场中做匀速圆周运动的半径为R，运动轨迹如答图2所示。
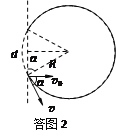
洛伦兹力提供向心力，根据牛顿第二定律有：
（1分）
解得：
（1分）
根据几何关系可知，O与N之间的距离
（1分）
（3）设粒子在电场中从M点运动至O点所用时为t1，
根据牛顿第二定律可知：粒子在电场中的加速度a=
（1分）
粒子通过O点时竖直方向速度vy=
，根据运动学公式有：vy=at1
解得：t1=
（1分）
设粒子在磁场中从O点运动至N点用时为t2，粒子在磁场中运动的周期
（1分）
解得：粒子从M点运动到N点的总时间t= t1+ t2=
+
【题目】如图所示，是某同学由打点计时器得到的表示小车运动过程的一条清晰纸带，纸带上两相邻计数点间还有四个点没有画出，打点计时器打点的频率f=50Hz，其中x1=7.05cm、x2=7.68cm、x3=8.33cm、x4=8.95cm、x5=9.61cm、x6=10.26cm．
（1）下表列出了打点计时器打下B、C、F时小车的瞬时速度，请在表中填入打点计时器打下D、E两点时小车的瞬时速度_____、______．（保留三位有效数字）
位置 | B | C | D | E | F |
速度（ms﹣1） | 0.737 | 0.801 | 0.994 |
（2）以A点为计时起点，在坐标图中画出小车的速度﹣时间图线___．
（3）根据你画出的小车的速度﹣时间图线计算出小车的加速度a=______m/s2．（保留两位有效数字）
（4）如果当时电网中交变电流的频率是f=49Hz，而做实验的同学并不知道，由此引起的系统误差将使加速度的测量值比实际值偏_____．（选填“大”或“小”）
