题目内容
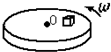 如图所示,水平转盘上放一小木块.角速度为1rad/s时,木块离轴8cm恰好与转盘无相对滑动,当角速度增加到2rad/s时,为使小木块刚好与转盘保持相对静止,那么木块应放在离轴多远的地方.
如图所示,水平转盘上放一小木块.角速度为1rad/s时,木块离轴8cm恰好与转盘无相对滑动,当角速度增加到2rad/s时,为使小木块刚好与转盘保持相对静止,那么木块应放在离轴多远的地方.分析:木块随圆盘恰好能做匀速圆周运动,由最大静摩擦力提供向心力,由牛顿第二定律求解最大静摩擦力.
若转速增加到2rad/s时,小木块刚好与转盘保持相对静止时,静摩擦力达到最大值,再由牛顿第二定律木块离轴的距离.
若转速增加到2rad/s时,小木块刚好与转盘保持相对静止时,静摩擦力达到最大值,再由牛顿第二定律木块离轴的距离.
解答:解:当角速度为ω1=1rad/s时,μmg=mω12r1 ①
当角速度为ω2=2rad/s时,μmg=mω22r2 ②
由①②两式可解得:r2=2cm
答:木块应放在离轴2cm的地方.
当角速度为ω2=2rad/s时,μmg=mω22r2 ②
由①②两式可解得:r2=2cm
答:木块应放在离轴2cm的地方.
点评:本题应用牛顿第二定律处理圆周运动的临界问题,关键分析临界条件:当物体刚要滑动时,静摩擦力达到最大值.

练习册系列答案
相关题目
 如图所示,水平转盘上的A、B、C三处有三块可视为质点的由同一种材料做成的正立方体物块;B、C处物块的质量相等为m,A处物块的质量为2m;A、B与轴O的距离相等,为r,C到轴O的距离为2r,转盘以某一角速度匀速转动时,A、B、C处的物块都没有发生滑动现象,下列说法中正确的是( )
如图所示,水平转盘上的A、B、C三处有三块可视为质点的由同一种材料做成的正立方体物块;B、C处物块的质量相等为m,A处物块的质量为2m;A、B与轴O的距离相等,为r,C到轴O的距离为2r,转盘以某一角速度匀速转动时,A、B、C处的物块都没有发生滑动现象,下列说法中正确的是( )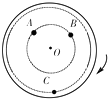 如图所示,水平转盘上的A、B、C三处有三块可视为质点的由同一种材料做成的正立方体物块;B、C处物块的质量相等,为m,A处物块的质量为2m;A、B与轴O的距离相等,为r,C到轴O的距离为2r,转盘以某一角速度匀速转动时,A、B、C处的物块都没有发生滑动现象,下列说法中正确的是( )
如图所示,水平转盘上的A、B、C三处有三块可视为质点的由同一种材料做成的正立方体物块;B、C处物块的质量相等,为m,A处物块的质量为2m;A、B与轴O的距离相等,为r,C到轴O的距离为2r,转盘以某一角速度匀速转动时,A、B、C处的物块都没有发生滑动现象,下列说法中正确的是( )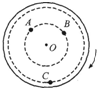 如图所示,水平转盘上的A、B、C三处有三块可视为质点正立方体物块,与转盘间的动摩擦因数相同,B、C处物块的质量相等为m,A处物块的质量为2m,点A、B与轴O的距离相等且为r,点C到轴O的距离为2r,转盘以某一角速度匀速转动时,A、B、C处的物块都没有发生滑动现象,下列说法中正确的是( )
如图所示,水平转盘上的A、B、C三处有三块可视为质点正立方体物块,与转盘间的动摩擦因数相同,B、C处物块的质量相等为m,A处物块的质量为2m,点A、B与轴O的距离相等且为r,点C到轴O的距离为2r,转盘以某一角速度匀速转动时,A、B、C处的物块都没有发生滑动现象,下列说法中正确的是( ) 如图所示,水平转盘上的A、B、C三处有三块可视为质点正立方体物块,与转盘间的动摩擦因数相同,B、C处物块的质量相等为m,A处物块的质量为2m,点A、B与轴O的距离相等且为r,点C到轴O的距离为2r,转盘以某一角速度匀速转动时,A、B、C处的物块都没有发生滑动现象,下列说法中正确的是( )
如图所示,水平转盘上的A、B、C三处有三块可视为质点正立方体物块,与转盘间的动摩擦因数相同,B、C处物块的质量相等为m,A处物块的质量为2m,点A、B与轴O的距离相等且为r,点C到轴O的距离为2r,转盘以某一角速度匀速转动时,A、B、C处的物块都没有发生滑动现象,下列说法中正确的是( ) 如图所示,水平转盘上有A、B两物体通过伸直细绳连接,A物置于转盘竖直转轴OO′上,A、B物体质量为别为3kg、1kg,A、B两物体与转盘间的动摩擦因素均为μ=0.1,细绳长度L=1m,设定A、B两物体与转盘间最大静摩擦力与滑动摩擦力相等,A、B两物体可视为质点,要使A、B两物体与转盘间不发生相对滑动,则转盘转动角速度不能超过( )
如图所示,水平转盘上有A、B两物体通过伸直细绳连接,A物置于转盘竖直转轴OO′上,A、B物体质量为别为3kg、1kg,A、B两物体与转盘间的动摩擦因素均为μ=0.1,细绳长度L=1m,设定A、B两物体与转盘间最大静摩擦力与滑动摩擦力相等,A、B两物体可视为质点,要使A、B两物体与转盘间不发生相对滑动,则转盘转动角速度不能超过( )