Question

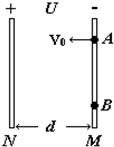两圆形平行金属板M、N，正对竖直放置，其半径r=0.3m，相距d=10cm，两板间加电压1000V；一个质量为m=0.02g，电量q=2×10^-8C的带电液滴，从M板上的A点，以初速度v₀=1m/s水平射向N板如图所示，恰好打在M板的B点，求：
（1）该圆形平行板电容器所带的电量；
（2）A、B两点间的距离为多少？
（3）带电液滴刚要打到B点时的速度？
（4）液滴运动过程中的最小速度是多少？
（g=10m/s²，静电力常量9×10⁹ Nm²/C²，空气介电常数为1）

Answer 1

分析：（1）根据电容的决定式C=

?S

4πkd

和定义式C=

Q

U

结合可求解电量；
（2）分析带电液滴在场中的运动，在水平方向受电场力qE，在竖直方向只受重力，做自由落体运动，有运动学公式可求解．
（3）根据动能定理求解带电液滴刚要打到B点时的速度．
（4）当液滴的合力与速度垂直时，速度最小，根据速度的分解法求解．

解答：解：（1）圆形金属棒面积为：S=πr²，
电容器的电容为：C=

?S

4πkd

=

1×π×0．32

4π×9×109×0.1

=2.5×10^-11F
则电容器所带的电量：Q=CU=2.5×10^-11×1000=2.5×10^-8C
（2）带电液滴在水平方向，受电场力qE作用，水平方向的加速度大小为：
a_x=

qU

md

=

2×10-8×1000

0.02×10-3×0.1

m/s²=10m/s²；
则运动时间为：t=

2v0

ax

=

2×1

10

s=0.2s
A、B两点间的距离为：h_AB=

1

2

gt2=

1

2

×10×0．22=0.2m
（3）根据动能定理得：mgh_AB=

1

2

m

v

2 B

-

1

2

m

v

2 0

得：v_B=

v 2 0 +2ghAB

=

12+2×10×0.2

m/s=

5

m/s
（4）当液滴的合力与速度垂直时，速度最小，由于a_x=g，则最小速度为：
v_min=v₀cos45°=1×

2

2

m/s=

2

2

m/s
答：（1）该圆形平行板电容器所带的电量为2.5×10^-8C；
（2）A、B两点间的距离为0.2m；
（3）带电液滴刚要打到B点时的速度是

5

m/s．
（4）液滴运动过程中的最小速度是

2

2

m/s．

点评：本题要掌握电容的两个公式：决定式C=

?S

4πkd

和定义式C=

Q

U

，正确分析带电液滴在场中的受力情况，运用正交分解法根据运动学公式和动能定理列式求解．