题目内容
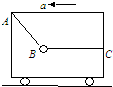
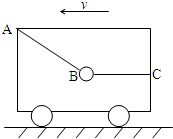
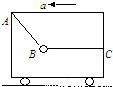
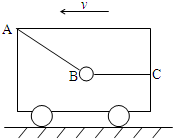 停在水平地面上的小车内,用绳子AB、BC栓住一个重球,绳BC呈水平状态,绳AB的拉力为T1,绳BC的拉力为T2.若小车由静止开始加速向左运动,但重球相对小车的位置不发生变化,则两绳的拉力的变化情况是( )
停在水平地面上的小车内,用绳子AB、BC栓住一个重球,绳BC呈水平状态,绳AB的拉力为T1,绳BC的拉力为T2.若小车由静止开始加速向左运动,但重球相对小车的位置不发生变化,则两绳的拉力的变化情况是( )分析:本题以小球为研究对象,分析受力,根据牛顿第二定律得到绳AB的拉力T1和绳BC的拉力T2与加速度的关系,即分析两绳拉力的变化情况.
解答:解:以小球为研究对象,分析受力:重力mg、绳AB的拉力T1和绳BC的拉力T2,如图.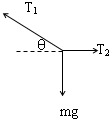
设小车的加速度为a,绳AB与水平方向的夹角为θ,根据牛顿第二定律得
T1sinθ=mg ①
T1cosθ-T2=ma ②
由①得 T1=
,
由②得 T2=mgtanθ-ma
可见,绳AB的拉力T1与加速度a无关,则T1保持不变.
绳BC的拉力T2随着加速度的增大而减小,则T2变小.故C正确.
故选C

设小车的加速度为a,绳AB与水平方向的夹角为θ,根据牛顿第二定律得
T1sinθ=mg ①
T1cosθ-T2=ma ②
由①得 T1=
| mg |
| sinθ |
由②得 T2=mgtanθ-ma
可见,绳AB的拉力T1与加速度a无关,则T1保持不变.
绳BC的拉力T2随着加速度的增大而减小,则T2变小.故C正确.
故选C
点评:本题在正确分析受力的基础上,根据牛顿第二定律,运用正交分解法研究两绳拉力的变化.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
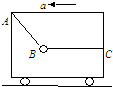 如图所示,停在水平地面上的小车内,用轻绳AB和BC拴住一个重球,绳BC呈水平状态,绳AB对球的拉力为T1,绳BC对球的拉力为T2.小车从静止开始向左加速运动,若重球相对小车位置不变,则两绳对球的拉力大小与车静止时相比( )
如图所示,停在水平地面上的小车内,用轻绳AB和BC拴住一个重球,绳BC呈水平状态,绳AB对球的拉力为T1,绳BC对球的拉力为T2.小车从静止开始向左加速运动,若重球相对小车位置不变,则两绳对球的拉力大小与车静止时相比( )