题目内容
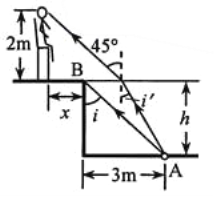
【题目】如图,在注满水的游泳池的池底有一点光源A,它到池边的水平距离为3.0 m。从点光源A射向池边的光线AB与竖直方向的夹角恰好等于全反射的临界角,水的折射率为![]() 。
。

(i)求池内的水深;
(ii)一救生员坐在离池边不远处的高凳上,他的眼睛到地面的高度为2.0 m。当他看到正前下方的点光源A时,他的眼睛所接受的光线与竖直方向的夹角恰好为45°。求救生员的眼睛到池边的水平距离(结果保留1位有效数字)。
【答案】(i)h=![]() m≈2.6 m;(ii)0.7 m
m≈2.6 m;(ii)0.7 m
【解析】试题分析:(i)如图,设达到池边的光线的入射角为i。依题意,水的折射率n=![]() ,光线的折射角θ=90°。
,光线的折射角θ=90°。
由折射定律有
nsin i="sin" θ①
由几何关系有
sin i=![]() ②
②
式中,l="3" m,h是池内水的深度。联立①②式并代入题给数据得
h=![]() m≈2.6 m③
m≈2.6 m③
(ii)设此时救生员的眼睛到池边的距离为x。依题意,救生员的视线与竖直方向的夹角为θ'=45°。由折射定律有
nsin i'="sin" θ' ④
式中,i'是光线在水面的入射角。设池底点光源A到水面入射点的水平距离为a。由几何关系有
sin i'=![]() ⑤
⑤
x+l=a+h' ⑥
式中h'="2" m。联立③④⑤⑥式得
x=(3![]() –1)m≈0.7 m⑦
–1)m≈0.7 m⑦

练习册系列答案
相关题目