题目内容
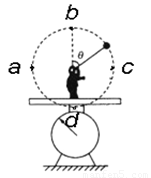
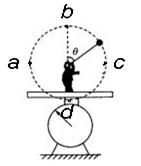
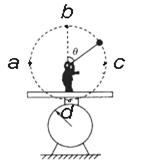
 如下图所示,一个质量为M的人,站在台秤上,一长为R的悬线一端系一个质量为m小球,手拿悬线另一端,小球绕悬线另一端点在竖直平面内做圆周运动,且小球恰好能通过圆轨道最高点,则下列说法正确是( )
如下图所示,一个质量为M的人,站在台秤上,一长为R的悬线一端系一个质量为m小球,手拿悬线另一端,小球绕悬线另一端点在竖直平面内做圆周运动,且小球恰好能通过圆轨道最高点,则下列说法正确是( )分析:因为小球正好通过圆轨道的最高点,这表示他在最高点时其重力mg正好提供其圆周运动所需的向心力,因此最低点时速度v可求,因此绳子拉力明显就是5mg,此时对人进行分析,其受到向下的重力,绳子的拉力5mg,再加上小球的重力为mg,台秤的支持力而保持平衡,所以F=(M+6m)g.
解答:解:A、小球恰好能通过圆轨道最高点,在最高点,细线中拉力为零,小球速度vb=
.小球从最高点运动到最低点,由机械能守恒定律,
+mg×2R=
,在最低点,由牛顿第二定律,F-mg=
,联立解得细线中拉力F=6mg.小球运动到最低点时,台秤的示数最大且为Mg+F=(M+6m)g,选项A正确;
B、小球运动到最高点时,细线中拉力为零,台秤的示数为Mg,但是不是最小,当小球处于如图所示状态时,
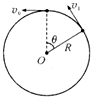
设其速度为v1,由牛顿第二定律有:T+mgcosθ=
解得悬线拉力 T=3mg(1-cosθ)
其分力Ty=Tcosθ=3mgcosθ-3mgcos2θ
当cosθ=0.5,即θ=60°时,
台秤的最小示数为Fmin=Mg-Ty=Mg-0.75mg.选项B错误;
C、小球在a、b、c三个位置,小球均处于完全失重状态,台秤的示数相同,选项C正确;
D、人没有运动,不会有超重失重状态,故D错误
故选:AC
| gR |
| 1 |
| 2 |
| mV | 2 b |
| 1 |
| 2 |
| mV | 2 d |
| ||
| R |
B、小球运动到最高点时,细线中拉力为零,台秤的示数为Mg,但是不是最小,当小球处于如图所示状态时,

设其速度为v1,由牛顿第二定律有:T+mgcosθ=
| ||
| R |
解得悬线拉力 T=3mg(1-cosθ)
其分力Ty=Tcosθ=3mgcosθ-3mgcos2θ
当cosθ=0.5,即θ=60°时,
台秤的最小示数为Fmin=Mg-Ty=Mg-0.75mg.选项B错误;
C、小球在a、b、c三个位置,小球均处于完全失重状态,台秤的示数相同,选项C正确;
D、人没有运动,不会有超重失重状态,故D错误
故选:AC
点评:本题考查了牛顿第二定律、动能定理的综合,关键知道圆周运动向心力的来源,选择合适的研究过程,运用动能定理、牛顿第二定律进行求解.

练习册系列答案
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目