题目内容
 (2011?永春县模拟)在一个水平面上建立x轴,过原点O垂直于x轴平面的右侧空间有一匀强电场,场强大小E=6×105 N/C,方向与x轴正方向相同.在O处放一个电荷量q=-5×10-6C,质量m=10g的绝缘物块,物块与水平面间的动摩擦因数μ=0.2,沿x轴正方向给物块一个初速度v0=2m/s,如图所示.求物块最终停止时的位置及整个过程运动的路程.(g取10m/s2)
(2011?永春县模拟)在一个水平面上建立x轴,过原点O垂直于x轴平面的右侧空间有一匀强电场,场强大小E=6×105 N/C,方向与x轴正方向相同.在O处放一个电荷量q=-5×10-6C,质量m=10g的绝缘物块,物块与水平面间的动摩擦因数μ=0.2,沿x轴正方向给物块一个初速度v0=2m/s,如图所示.求物块最终停止时的位置及整个过程运动的路程.(g取10m/s2)分析:先求出滑动摩擦力和电场力,通过比较,判断出物体的运动规律;然后对向右的减速过程和向左的总过程运用动能定理列式求解,得出物体的运动轨迹和总路程.
解答: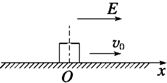 解:物体受到的电场力为:F=Eq=6×105×5×10-6=3 N,方向水平向左.
解:物体受到的电场力为:F=Eq=6×105×5×10-6=3 N,方向水平向左.
物体受到的摩擦力为:f=μmg=0.2×0.01×10=0.02 N
∵F>f∴物块先向右减速运动,再向左加速运动,越过O点进入无电场区域后,再减速运动直到停止.
设物块到达最右端的坐标为x1 m,对O→x1 m处,由动能定理得:
-F?x1-f?x1=0-
m
即:3x1+0.02x1=
×0.01×4
∴x1=
m
设物块最终停止的位置坐标为-x2 m,对O→-x2 m处,
由动能定理得:-2f?x1-f?x2=0-
m
即:2×0.02×
+0.02x2=
×0.01×4
∴x2=
m
即物块停在-
m处,且总路程为S=
×2+
=1m.
 解:物体受到的电场力为:F=Eq=6×105×5×10-6=3 N,方向水平向左.
解:物体受到的电场力为:F=Eq=6×105×5×10-6=3 N,方向水平向左.物体受到的摩擦力为:f=μmg=0.2×0.01×10=0.02 N
∵F>f∴物块先向右减速运动,再向左加速运动,越过O点进入无电场区域后,再减速运动直到停止.
设物块到达最右端的坐标为x1 m,对O→x1 m处,由动能定理得:
-F?x1-f?x1=0-
| 1 |
| 2 |
| v | 2 0 |
即:3x1+0.02x1=
| 1 |
| 2 |
∴x1=
| 1 |
| 151 |
设物块最终停止的位置坐标为-x2 m,对O→-x2 m处,
由动能定理得:-2f?x1-f?x2=0-
| 1 |
| 2 |
| v | 2 0 |
即:2×0.02×
| 1 |
| 151 |
| 1 |
| 2 |
∴x2=
| 149 |
| 151 |
即物块停在-
| 149 |
| 151 |
| 1 |
| 151 |
| 149 |
| 151 |
点评:本题关键先对物体受力分析得出物体的运动规律,然后选择不同的物理过程运用动能定理列式求解.

练习册系列答案
相关题目
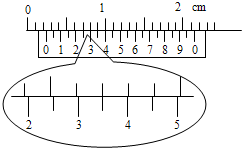
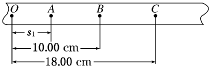 (2011?永春县模拟)在做“研究匀变速直线运动”的实验中,取下一段如图所示的纸带研究其运动情况.设O点为计数的起始点,在四个连续的计数点中,相邻两计数点间的时间间隔为0.1s,若物体做理想的匀加速直线运动,则计数点A与起始点O之间的距离s1为
(2011?永春县模拟)在做“研究匀变速直线运动”的实验中,取下一段如图所示的纸带研究其运动情况.设O点为计数的起始点,在四个连续的计数点中,相邻两计数点间的时间间隔为0.1s,若物体做理想的匀加速直线运动,则计数点A与起始点O之间的距离s1为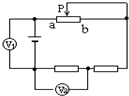 (2011?永春县模拟)如图所示的电路中,电源的电动势为E,内阻为r.当可变电阻的滑片P向b移动时,电压表V1的示数U1与电压表V2的示数U2的变化情况是( )
(2011?永春县模拟)如图所示的电路中,电源的电动势为E,内阻为r.当可变电阻的滑片P向b移动时,电压表V1的示数U1与电压表V2的示数U2的变化情况是( )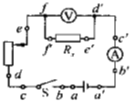 (2011?永春县模拟)在做“测定金属的电阻率”的实验时,有位同学按图所示电路进行连线,他共用7根导线:ab、cd、ef、ff′、e′d′、d′c′、b′a′,由于其中有一根内部断开的导线,所以当他合上开关S后,无论怎样移动滑动变阻器的滑片,电压表读数都约为4.5V,电流表读数接近零.
(2011?永春县模拟)在做“测定金属的电阻率”的实验时,有位同学按图所示电路进行连线,他共用7根导线:ab、cd、ef、ff′、e′d′、d′c′、b′a′,由于其中有一根内部断开的导线,所以当他合上开关S后,无论怎样移动滑动变阻器的滑片,电压表读数都约为4.5V,电流表读数接近零.