题目内容
5.一颗人造卫星在离地面高度等于地球半径的圆形轨道上运行,已知地球的第一宇宙速度为v1=7.9km/s,地球表面重力加速度为g=9.8m/s2.求:(1)这颗卫星运行的线速度为多大?
(2)它绕地球运动的向心加速度为多大?
分析 (1)此题为卫星做圆周运动的基本计算型题目,根据万有引力提供向心力列式,求解线速度.
(2)由牛顿第二定律和万有引力等于重力列式,求解向心加速度.
解答 解:(1)人造地球卫星在圆形轨道上运行时,由万有引力提供向心力,则有:
$G\frac{Mm}{{r}^{2}}=m\frac{{v}^{2}}{r}$
解得,v=$\sqrt{\frac{GM}{2R}}$
对于卫星的第一宇宙速度有:v1=$\sqrt{\frac{GM}{R}}$
代入数据解得:v=5.58km/s
(2)根据牛顿第二定律得:
ma=$G\frac{Mm}{{r}^{2}}$,
得加速度为:a=$G\frac{M}{{r}^{2}}$=$G\frac{M}{{(2R)}^{2}}$
又mg=$G\frac{Mm}{{R}^{2}}$
联立是两式得:a=$\frac{g}{4}$=2.45m/s2
答:(1)这颗卫星运行的线速度为5.58km/s;
(2)它绕地球运动的向心加速度为2.45m/s2
点评 此题为卫星做圆周运动的基本计算型题目,主要考查万有引力充当向心力和万有引力等于重力的相关应用和计算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.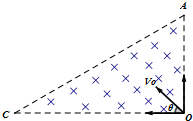 如图所示,以直角三角形AOC为边界的有界匀强磁场区域,磁感应强度为B,∠A=60°,AO=a.在O 点放置一个粒子源,可以向各个方向发射某种带负电粒子,粒子的比荷为$\frac{q}{m}$,发射速度大小都为v0,且满足v0=$\frac{qBa}{m}$,发射方向由图中的角度θ表示.对于粒子进入磁场后的运动(不计重力作用),下列说法正确的是( )
如图所示,以直角三角形AOC为边界的有界匀强磁场区域,磁感应强度为B,∠A=60°,AO=a.在O 点放置一个粒子源,可以向各个方向发射某种带负电粒子,粒子的比荷为$\frac{q}{m}$,发射速度大小都为v0,且满足v0=$\frac{qBa}{m}$,发射方向由图中的角度θ表示.对于粒子进入磁场后的运动(不计重力作用),下列说法正确的是( )
 如图所示,以直角三角形AOC为边界的有界匀强磁场区域,磁感应强度为B,∠A=60°,AO=a.在O 点放置一个粒子源,可以向各个方向发射某种带负电粒子,粒子的比荷为$\frac{q}{m}$,发射速度大小都为v0,且满足v0=$\frac{qBa}{m}$,发射方向由图中的角度θ表示.对于粒子进入磁场后的运动(不计重力作用),下列说法正确的是( )
如图所示,以直角三角形AOC为边界的有界匀强磁场区域,磁感应强度为B,∠A=60°,AO=a.在O 点放置一个粒子源,可以向各个方向发射某种带负电粒子,粒子的比荷为$\frac{q}{m}$,发射速度大小都为v0,且满足v0=$\frac{qBa}{m}$,发射方向由图中的角度θ表示.对于粒子进入磁场后的运动(不计重力作用),下列说法正确的是( )| A. | 粒子在磁场中运动最长时间为$\frac{πa}{3{v}_{0}}$ | |
| B. | 粒子在磁场中运动最短时间为$\frac{πm}{3Bq}$ | |
| C. | 在AC 边界上只有一半区域有粒子射出 | |
| D. | 在三角形AOC边界上,有粒子射出的边界线总长为2a |
16.2007年10月24日18时05分,我国成功发射了“嫦娥一号”探月卫星,11月5日进入月球轨道后,经历3次轨道调整,进入工作轨道.若该卫星在地球表面的重力为G1,在月球表面的重力为G2,已知地球半径为R1,月球半径为R2,地球表面处的重力加速度为g,则( )
| A. | 月球表面处的重力加速度g月为$\frac{{G}_{1}}{{G}_{2}}$g | |
| B. | 月球的质量与地球的质量之比为$\frac{{G}_{2}{R}_{2}^{2}}{{G}_{1}{R}_{1}^{2}}$ | |
| C. | 卫星在距月球表面轨道上做匀速圆周运动的周期T月为2π$\sqrt{\frac{{R}_{2}{G}_{1}}{g{G}_{2}}}$ | |
| D. | 月球的第一宇宙速度与地球的第一宇宙速度之比为$\sqrt{\frac{{G}_{1}{R}_{2}}{{G}_{2}{R}_{1}}}$ |
20.对下列现象的解释中不正确的是( )
| A. | 两块铁经过高温加压将连成一整块,这说明铁分子间有吸引力 | |
| B. | 一定质量的气体能充满整个容器,这说明在一般情况下,气体分子间的作用力很微弱 | |
| C. | 电焊能把两块金属连接成一整块是分子间的引力起作用 | |
| D. | 破碎的玻璃不能把它们拼接在一起是因为其分子间斥力作用的结果 |
10.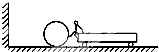 如图所示,载人小车和弹性球静止在光滑长直水平面上,球的质量为m,人与车的总质量为20m,人将球以对地水平速率v推向竖直墙壁,球又以速率v弹回,人接住球后再以速率v将球推向墙壁,如此反复,人经几次推球后,再也不能接住球( )
如图所示,载人小车和弹性球静止在光滑长直水平面上,球的质量为m,人与车的总质量为20m,人将球以对地水平速率v推向竖直墙壁,球又以速率v弹回,人接住球后再以速率v将球推向墙壁,如此反复,人经几次推球后,再也不能接住球( )
 如图所示,载人小车和弹性球静止在光滑长直水平面上,球的质量为m,人与车的总质量为20m,人将球以对地水平速率v推向竖直墙壁,球又以速率v弹回,人接住球后再以速率v将球推向墙壁,如此反复,人经几次推球后,再也不能接住球( )
如图所示,载人小车和弹性球静止在光滑长直水平面上,球的质量为m,人与车的总质量为20m,人将球以对地水平速率v推向竖直墙壁,球又以速率v弹回,人接住球后再以速率v将球推向墙壁,如此反复,人经几次推球后,再也不能接住球( )| A. | 9次 | B. | 10次 | C. | 11次 | D. | 12次 |
17.下列关于做匀速圆周运动的物体说法中正确的是( )
| A. | 线速度大小和方向都不变 | B. | 加速度大小和方向都不变 | ||
| C. | 向心力大小和方向都不变 | D. | 向心力就是物体受到的合力 |
2. 如图所示,两带电平行金属板之间有相互正交的匀强电场和匀强磁场.现使一个带正电的粒子以某一初速沿垂直于电场和磁场的方向射入两极板间,测得它飞出该场区时的动能比射入时的动能小.为使带电粒子飞出场区时的动能比射入时的动能大,以下措施中可行的是( )
如图所示,两带电平行金属板之间有相互正交的匀强电场和匀强磁场.现使一个带正电的粒子以某一初速沿垂直于电场和磁场的方向射入两极板间,测得它飞出该场区时的动能比射入时的动能小.为使带电粒子飞出场区时的动能比射入时的动能大,以下措施中可行的是( )
 如图所示,两带电平行金属板之间有相互正交的匀强电场和匀强磁场.现使一个带正电的粒子以某一初速沿垂直于电场和磁场的方向射入两极板间,测得它飞出该场区时的动能比射入时的动能小.为使带电粒子飞出场区时的动能比射入时的动能大,以下措施中可行的是( )
如图所示,两带电平行金属板之间有相互正交的匀强电场和匀强磁场.现使一个带正电的粒子以某一初速沿垂直于电场和磁场的方向射入两极板间,测得它飞出该场区时的动能比射入时的动能小.为使带电粒子飞出场区时的动能比射入时的动能大,以下措施中可行的是( )| A. | 增大粒子射入时的速度 | |
| B. | 保持金属极板所带电荷量不变,增大两板间的距离 | |
| C. | 保持两极板间的距离不变,增大两金属极板所带的电荷量 | |
| D. | 减小磁场的磁感应强度 |
3.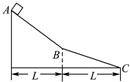 如图所示,一小物块在粗糙程度相同的两个固定斜面上从A经B滑动到C,如不考虑在B点机械能的损失,则( )
如图所示,一小物块在粗糙程度相同的两个固定斜面上从A经B滑动到C,如不考虑在B点机械能的损失,则( )
 如图所示,一小物块在粗糙程度相同的两个固定斜面上从A经B滑动到C,如不考虑在B点机械能的损失,则( )
如图所示,一小物块在粗糙程度相同的两个固定斜面上从A经B滑动到C,如不考虑在B点机械能的损失,则( )| A. | 从A到B和从B到C,减少的机械能相等 | |
| B. | 从A到B和从B到C,增加的动能相等 | |
| C. | 从A到B和从B到C,摩擦产生的热量相等 | |
| D. | 小物块在B点的动能一定最大 |