题目内容
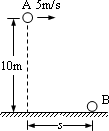
某人以2 m/s的初速度将质量为4 kg的小球水平抛出,小球落地时的速度为4 m/s,求:(1)小球刚被抛出时离地面的高度为多少?(2)人抛小球时,对球所做的功为多少?(取g = 10 m/s2,空气阻力不计)
【答案】
(1)设刚抛小球离地面高度为h,物体的质量为m,并以地面为零势面。
EP1 = mgh,Ek1 = mV02/2,EP2 = 0,Ek2 = mV2/2,由于在整个过程只有重力做功,根据机械能守恒定律得:mV02/ 2 + mgh = mV2/ 2,………………(3分)
∴刚抛小球时离地面的高度为:
h = (V2 —V02)/ 2g = ( 42 — 22 ) / 2×10 = 0.6(m),……………………(3分)
(2)人对小球做功,小球获得了动能
∴W = mV02/ 2 = 4×22 / 2 = 8(J)。……………………………………(4分)
【解析】(1)设刚抛小球离地面高度为h,物体的质量为m,并以地面为零势面。
EP1 = mgh,Ek1 = mV02/2,EP2 = 0,Ek2 = mV2/2,由于在整个过程只有重力做功,根据机械能守恒定律得:mV02/ 2 + mgh = mV2/ 2,………………(3分)
∴刚抛小球时离地面的高度为:
h = (V2 —V02)/ 2g = ( 42 — 22 ) / 2×10 = 0.6(m),……………………(3分)
(2)人对小球做功,小球获得了动能
∴W = mV02/ 2 = 4×22 / 2 = 8(J)。……………………………………(4分)

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目