题目内容
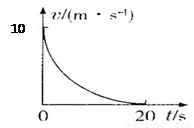
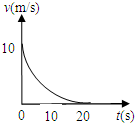 一质点沿直线运动,其速度随时间变化的关系图象即v-t图象,恰好是与两坐标轴相切的四分之一圆弧,切点的坐标分别为(0,10 )和(20,0).如图所示,则该质点在这20s内位移为________m,该质点在第10s末时的加速度大小为________m/s2.
一质点沿直线运动,其速度随时间变化的关系图象即v-t图象,恰好是与两坐标轴相切的四分之一圆弧,切点的坐标分别为(0,10 )和(20,0).如图所示,则该质点在这20s内位移为________m,该质点在第10s末时的加速度大小为________m/s2.
43 0.29
分析:由图读出速度的变化情况,分析物体的运动情况.速度图象的斜率等于加速度.由图线“面积”求出位移,根据运动学基本公式及几何关系求解.
解答: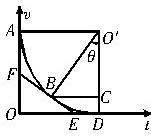 解:由图线“面积”表示位移得:S=10×
解:由图线“面积”表示位移得:S=10×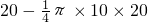 m=43m
m=43m
该质点在第10s末时的加速度大小为a=k=0.29m/s2.
如图所示,过10s对应的圆弧上的B点作切线EF,设圆弧的半径为R,由图形方面考虑,易得
sinθ=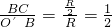 ,解得θ=30°由图中几何关系可知,△EOF~△O′CB,故
,解得θ=30°由图中几何关系可知,△EOF~△O′CB,故
tanθ=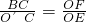
因速度图象的斜率表示加速度的大小,则
a=tan∠OEF=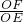 =
=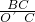
由加速度的概念知:BC应表示的是速度,O′C表示的是时间.
在△O′BC中,BC=O′Bsinθ,因BC表示的是速度,故O′B=O′D=AO=8(m/s),BC=8?sin30°=4(m/s).
在△O′BC中,O′C=O′Bcosθ,因O′C表示的是时间,故O′B=O′A=DO=20(s)
O′C=20?cos30°=10 (s)
(s)
所以加速度a=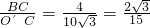 =0.29(m/s2)
=0.29(m/s2)
故答案为:43,0.29.
点评:本题关键抓住速度图象的斜率表示加速度、“面积”表示位移来理解图象的物理意义,并能结合几何关系求解,难度较大.
分析:由图读出速度的变化情况,分析物体的运动情况.速度图象的斜率等于加速度.由图线“面积”求出位移,根据运动学基本公式及几何关系求解.
解答:
 解:由图线“面积”表示位移得:S=10×
解:由图线“面积”表示位移得:S=10×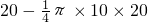 m=43m
m=43m该质点在第10s末时的加速度大小为a=k=0.29m/s2.
如图所示,过10s对应的圆弧上的B点作切线EF,设圆弧的半径为R,由图形方面考虑,易得
sinθ=
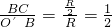 ,解得θ=30°由图中几何关系可知,△EOF~△O′CB,故
,解得θ=30°由图中几何关系可知,△EOF~△O′CB,故tanθ=
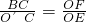
因速度图象的斜率表示加速度的大小,则
a=tan∠OEF=
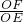 =
=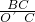
由加速度的概念知:BC应表示的是速度,O′C表示的是时间.
在△O′BC中,BC=O′Bsinθ,因BC表示的是速度,故O′B=O′D=AO=8(m/s),BC=8?sin30°=4(m/s).
在△O′BC中,O′C=O′Bcosθ,因O′C表示的是时间,故O′B=O′A=DO=20(s)
O′C=20?cos30°=10
 (s)
(s)所以加速度a=
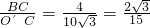 =0.29(m/s2)
=0.29(m/s2)故答案为:43,0.29.
点评:本题关键抓住速度图象的斜率表示加速度、“面积”表示位移来理解图象的物理意义,并能结合几何关系求解,难度较大.

练习册系列答案
相关题目
 一质点沿直线运动,其v-t图象如图所示.由图象可知( )
一质点沿直线运动,其v-t图象如图所示.由图象可知( )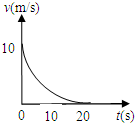 一质点沿直线运动,其速度随时间变化的关系图象即v-t图象,恰好是与两坐标轴相切的四分之一圆弧,切点的坐标分别为(0,10 )和(20,0).如图所示,则该质点在这20s内位移为
一质点沿直线运动,其速度随时间变化的关系图象即v-t图象,恰好是与两坐标轴相切的四分之一圆弧,切点的坐标分别为(0,10 )和(20,0).如图所示,则该质点在这20s内位移为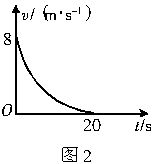
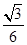 m/s2
m/s2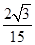 m/s2
m/s2