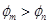题目内容
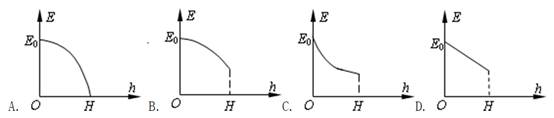
在光滑绝缘的水平面上固定有一点电荷,A、B是该点电荷场中一条电场线上的两点,带负电的小球沿该电场线从A点运动到B点,其动能随位置变化的关系如图8所示.设A、B两点的电势分别为φA、φB,小球在A、B两点的电势能分别为EpA、EpB,则关于点电荷的位置及电势、小球电势能大小的说法正确的是( ).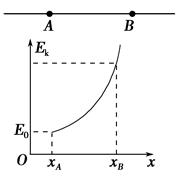
A.点电荷带正电在B点右侧
B.点电荷带负电在B点右侧
C.φA<φB、EpA>EpB
D.φA>φB、EpA<EpB
AC
解析试题分析:由图像的弯曲方向和动能定理 可知:小球从A到B电场力越来越大,所以点电荷应该在B点一侧;又因为小球动能越来越大,电场力做正功,点电荷是正电荷,故选项A正确B错误;由上面的分析可知电场方向从B指向A,所以A点的电势小于B点的电势;电场力做正功,电势能减小,即A点的电势能大于B点的电势能,故选项C正确.
可知:小球从A到B电场力越来越大,所以点电荷应该在B点一侧;又因为小球动能越来越大,电场力做正功,点电荷是正电荷,故选项A正确B错误;由上面的分析可知电场方向从B指向A,所以A点的电势小于B点的电势;电场力做正功,电势能减小,即A点的电势能大于B点的电势能,故选项C正确.
考点:解答本题的关键在于根据图像能分析出小球运动过程中电场力的大小变化和方向,进而分析电势的大小关系及结合电场力做功的情况分析电势能的变化.

电荷量分别为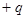 、
、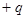 、
、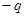 的三个带电小球,分别固定在边长均为L的绝缘三角形框架的三个顶点上,并置于场强为E的匀强电场中,如图所示.若三角形绕穿过其中心O垂直于三角形所在平面的轴顺时针转过120°,则此过程中系统电势能变化情况为
的三个带电小球,分别固定在边长均为L的绝缘三角形框架的三个顶点上,并置于场强为E的匀强电场中,如图所示.若三角形绕穿过其中心O垂直于三角形所在平面的轴顺时针转过120°,则此过程中系统电势能变化情况为 
A.减少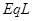 | B.增加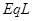 |
C.减少  | D.增加 |
如图所示,a、b、c、d是某匀强电场中的四个点,它们正好是一个矩形的四个顶点,ab=cd=L,ad=bc=2L,电场线与矩形所在平面平行. 已知a点电势为20 V,b点电势为24 V,d点电势为12 V.一个质子从b点以v0的速度射入此电场,入射方向与bc成45°,一段时间后经过c点.不计质子的重力.下列判断正确的是:( )
| A.c点电势为16V |
| B.场强的方向由b指向d |
C.质子从b运动到c所用的时间为 |
| D.质子从b运动到c,电场力做功为8 eV |
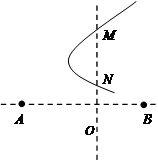
某静电场的电场线分布如图所示,图中P、Q两点的电场强度的大小分别为EP和EQ,电势分别为φP和φQ,则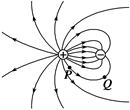
| A.EP<EQ,φP>φQ |
| B.EP>EQ,φP<φQ |
| C.EP>EQ,φP>φQ |
| D.EP<EQ,φP<φQ |
如图所示,虚线表示某电场的等势面.一带电粒子仅在电场力作用下由A运动到B的径迹如图中实线所示.粒子在A点的加速度为aA、电势能为EA;在B点的加速度为aB、电势能为EB.则下列结论正确的是( )
| A.粒子带正电,aA>aB,EA>EB |
| B.粒子带负电,aA>aB,EA>EB |
| C.粒子带正电,aA<aB,EA<EB |
| D.粒子带负电,aA<aB,EA<EB |

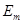 、
、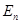 ,电势分别为
,电势分别为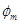 、
、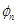 ,取无穷远为零电势.下列说法中正确的是:( )
,取无穷远为零电势.下列说法中正确的是:( )