题目内容
15. 如图所示,处于匀强磁场中的两根足够长、电阻不计的平行金属导轨相距1m,导轨平面与水平面成θ=37°角,下端连接阻值为R的电阻.匀强磁场方向与导轨平面垂直向上.质量为0.2kg,电阻不计的金属棒放在两导轨上,棒与导轨垂直并保持良好接触,它们之间的动摩擦因数为0.25.
如图所示,处于匀强磁场中的两根足够长、电阻不计的平行金属导轨相距1m,导轨平面与水平面成θ=37°角,下端连接阻值为R的电阻.匀强磁场方向与导轨平面垂直向上.质量为0.2kg,电阻不计的金属棒放在两导轨上,棒与导轨垂直并保持良好接触,它们之间的动摩擦因数为0.25.(1)求金属棒沿导轨由静止开始下滑时的加速度大小;
(2)当金属棒下滑速度达到稳定时,电阻R消耗的功率为8W,求该速度的大小;
(3)在第二问中,如果R=2Ω,金属棒中的电流方向由a到b,求磁感应强度的大小和方向.(g=10m/s2,sin37°=0.6,cos37°=0.8)
分析 (1)开始下滑时,速度为零,无感应电流产生,因此不受安培力,故根据牛顿第二定律可直接求解结果.
(2)金属棒下滑速度达到稳定时,金属棒所受合外力为零,根据平衡条件求出安培力,然后根据公式P=Fv求解.
(3)结合第(2)问求出回路中的感应电流,然后根据电功率的公式求解.
解答 解:(1)金属棒开始下滑的初速为零,根据牛顿第二定律有:
mgsinθ-μmgcosθ=ma…①
由①式解得:a=g(sinθ-μcosθ)=10×(O.6-0.25×0.8)m/s2=4m/s2…②
故金属棒沿导轨由静止开始下滑时的加速度大小为4m/s2.
(2)设金属棒运动达到稳定时,速度为v,所受安培力为F,棒在沿导轨方向受力平衡,有:
mgsinθ-μmgcosθ-F=0…③
此时金属棒克服安培力做功的功率等于电路中电阻R消耗的电功率:P=Fv…④
由③、④两式解得:v=$\frac{P}{F}$=$\frac{P}{mg(sinθ-μcosθ)}$=$\frac{8}{0.2×10×(0.6-0.25×0.8)}$m/s=10m/s…⑤
故当金属棒下滑速度达到稳定时,棒的速度大小为10m/s.
(3)设电路中电流为I,两导轨间金属棒的长为l,
磁场的磁感应强度为B,感应电流为:
I=$\frac{E}{R}$=$\frac{BLv}{R}$…⑥
功率为:P=I2R…⑦
由⑥、⑦两式解得:B=0.4T…⑧
故磁感应强度的大小为0.4T,方向垂直导轨平面向上.
答:(1)金属棒沿导轨由静止开始下滑时的加速度大小为4m/s2;
(2)该速度的大小为10m/s;
(3)在上问中,若R=2Ω,磁感应强度的大小为0.4T,磁场方向垂直导轨平面向上.
点评 解这类问题的突破口为正确分析安培力的变化,正确分析导体棒的运动状态,从力和功率两个角度进行列方程求解.

| A. | 运动物体的加速度不变,则其运动状态一定不变 | |
| B. | 物体的位置在不断变化,则其运动状态一定在不断变化 | |
| C. | 做直线运动的物体,其运动状态一定不变 | |
| D. | 运动物体的速度不变,其运动状态一定不变 |
 高温超导限流器由超导部件和限流电阻并联组成,如图.超导部件有一个超导临界电流Ic,当通过限流器的电流I>Ic时,将造成超导体失超,从超导态(电阻为零)转变为正常态(一个纯电阻).以此来限制电力系统的故障电流,已知超导部件的正常态电阻为R1=3Ω,超导临界电流Ic=1.2A,限流电阻R2=6Ω,小灯泡L上标有“6V,6W”的字样,电源电动势E=8V,内阻r=2Ω,原来电路正常工作,现L突然发生短路,则( )
高温超导限流器由超导部件和限流电阻并联组成,如图.超导部件有一个超导临界电流Ic,当通过限流器的电流I>Ic时,将造成超导体失超,从超导态(电阻为零)转变为正常态(一个纯电阻).以此来限制电力系统的故障电流,已知超导部件的正常态电阻为R1=3Ω,超导临界电流Ic=1.2A,限流电阻R2=6Ω,小灯泡L上标有“6V,6W”的字样,电源电动势E=8V,内阻r=2Ω,原来电路正常工作,现L突然发生短路,则( )| A. | 短路前通过R1的电流为$\frac{2}{3}$A | |
| B. | 短路后超导部件将由超导状态转化为正常态 | |
| C. | 短路后通过R1的电流为$\frac{4}{3}$A | |
| D. | 短路后通过R1的电流为2A |
| A. | 人的动能增加了1000J | B. | 人的动能增加了5000 J | ||
| C. | 人的机械能增加了5000 J | D. | 电梯对人做功6000 J |
| A. | 布朗运动是水分子在做剧烈热运动的反映 | |
| B. | 布朗运动是小炭粒分子之间相互渗透的结果 | |
| C. | 小炭粒越小,布朗运动越剧烈 | |
| D. | 小炭粒越小,布朗运动越不剧烈 |
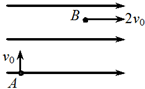 如图所示,质量为m带电量为q的带电微粒,以初速度v0从A点竖直向上射入真空中的沿水平方向的匀强电场中,微粒通过电场中B点时速率vB=2v0,方向与电场的方向一致,则下列选项正确的是( )
如图所示,质量为m带电量为q的带电微粒,以初速度v0从A点竖直向上射入真空中的沿水平方向的匀强电场中,微粒通过电场中B点时速率vB=2v0,方向与电场的方向一致,则下列选项正确的是( )| A. | 微粒所受的电场力大小是其所受重力的2倍 | |
| B. | 带电微粒的机械能增加了mv02 | |
| C. | A、B两点间的电势差为$\frac{2m{{v}_{0}}^{2}}{q}$ | |
| D. | A、B两点间的电势差为$\frac{3m{{v}_{0}}^{2}}{2q}$ |
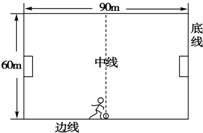 足球比赛中,经常使用“边路突破,下底传中”的战术,即攻方队员带球沿边线前进,到底线附近进行传中.某足球场长90m、宽60m.攻方前锋在中线处将足球沿边线向前踢出,足球的运动可视为在地面上做初速度为12m/s的匀减速直线运动,加速度大小为2m/s2.试求:
足球比赛中,经常使用“边路突破,下底传中”的战术,即攻方队员带球沿边线前进,到底线附近进行传中.某足球场长90m、宽60m.攻方前锋在中线处将足球沿边线向前踢出,足球的运动可视为在地面上做初速度为12m/s的匀减速直线运动,加速度大小为2m/s2.试求: