题目内容
20. 如图所示,倾角为α,斜面光滑的三角劈M放在光滑的水平面上,当用一个水平恒力F推三角劈时,其斜面上质量为m的物体与三角劈保持相对静止,以下说法正确的是( )
如图所示,倾角为α,斜面光滑的三角劈M放在光滑的水平面上,当用一个水平恒力F推三角劈时,其斜面上质量为m的物体与三角劈保持相对静止,以下说法正确的是( )| A. | 力F的大小为(M+m)gtanα | B. | 物体m受到的合外力大小为$\frac{mF}{M+m}$ | ||
| C. | 物体m受到的合外力大小为零 | D. | 物体m对斜面的压力大小$\frac{Fm}{(M+m)sinα}$ |
分析 对物块受力分析,其受到两个力的作用:重力,斜面支持力.由受力分解和牛顿第二定律可以得到斜面对m的弹力的两个表达式.
解答 解:先对滑块m受力分析,受重力和支持力,合力水平向左,如图所示: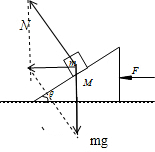
故物体m受到的合外力大小为:
F1=mgtanθ ①
N=$\frac{mg}{cosθ}$ ②
再对斜面体和滑块整体分析,根据牛顿第二定律,有:
F=(M+m)a ③
对m,根据牛顿第二定律,有:
F1=ma ④
A、C、联立①③④解得:F=(M+m)gtanα,故A正确,C错误;
B、联立①③④解得:F1=$\frac{mF}{M+m}$,故B正确;
D、对物体m,支持力为:N=$\frac{{F}_{1}}{sinθ}$,由于F1=$\frac{mF}{M+m}$,故N=$\frac{Fm}{(M+m)sinα}$;根据牛顿第三定律,压力也为$\frac{Fm}{(M+m)sinα}$;故D正确;
故选:ABD.
点评 解决本题的关键能够正确地受力分析,运用牛顿第二定律进行求解,注意整体法和隔离法的运用.

练习册系列答案
相关题目
8.奥运会中的投掷的链球、铅球、铁饼和标枪等体育比赛项目都是把物体斜向上抛出的运动,这些物体从抛出到落地的过程中(不计空气阻力)( )


| A. | 物体的机械能一直减小 | |
| B. | 物体的机械能不变 | |
| C. | 物体的动能先增大后减小,重力势能先减小后增大 | |
| D. | 物体的动能先减小后增大,重力势能先增大后减小 |
9.如图所示,ab是闭合电路的一部分,处在垂直于纸面向外的匀强磁场中( )


| A. | 当ab垂直于纸面向外平动时,ab中有感应电流 | |
| B. | 当ab垂直于纸面向里平动时,ab中有感应电流 | |
| C. | 当ab垂直于磁感线向右平动时,ab中有感应电流 | |
| D. | 当ab垂直于磁感线向左平动时,ab中无感应电流 |
5. 如图所示,金属环半径为a,总电阻为R,匀强磁场磁感应强度为B,垂直穿过环平面.电阻为$\frac{R}{2}$的导体杆AB,沿环表面以速度v向右滑至环中央时,A、B两点间的电压为( )
如图所示,金属环半径为a,总电阻为R,匀强磁场磁感应强度为B,垂直穿过环平面.电阻为$\frac{R}{2}$的导体杆AB,沿环表面以速度v向右滑至环中央时,A、B两点间的电压为( )
 如图所示,金属环半径为a,总电阻为R,匀强磁场磁感应强度为B,垂直穿过环平面.电阻为$\frac{R}{2}$的导体杆AB,沿环表面以速度v向右滑至环中央时,A、B两点间的电压为( )
如图所示,金属环半径为a,总电阻为R,匀强磁场磁感应强度为B,垂直穿过环平面.电阻为$\frac{R}{2}$的导体杆AB,沿环表面以速度v向右滑至环中央时,A、B两点间的电压为( )| A. | Bav | B. | $\frac{Bav}{2}$ | C. | $\frac{2Bav}{3}$ | D. | $\frac{4Bav}{3}$ |
 如图所示,平台离水平地面的高度为H=5m,一质量为m=1kg的小球从平台上A点以某一速度水平抛出,测得其运动到B点时的速度为vB=10m/s.已知B点离地面的高度为h=1.8m,取重力加速度g=10m/s2,以水平地面为零势能面.问:
如图所示,平台离水平地面的高度为H=5m,一质量为m=1kg的小球从平台上A点以某一速度水平抛出,测得其运动到B点时的速度为vB=10m/s.已知B点离地面的高度为h=1.8m,取重力加速度g=10m/s2,以水平地面为零势能面.问: 将长方形匀质薄板锯成如图所示的三部分,其中B、C两部分完全对称,现将三块拼在一起平放在粗糙的水平面上,当与板左侧垂直的水平力F作用于薄板时,薄板恰能水平向右匀速运动,且B与A,C与A之间没有相对滑动,图中的θ角为已知,求A与B之间的压力为多少?
将长方形匀质薄板锯成如图所示的三部分,其中B、C两部分完全对称,现将三块拼在一起平放在粗糙的水平面上,当与板左侧垂直的水平力F作用于薄板时,薄板恰能水平向右匀速运动,且B与A,C与A之间没有相对滑动,图中的θ角为已知,求A与B之间的压力为多少? 如图所示,一矩形线框abcd放在匀强磁场中,当线框绕轴oo′转动时有感应电流产生,当线框绕轴ab转动时无 感应电流产生.(填有、无)
如图所示,一矩形线框abcd放在匀强磁场中,当线框绕轴oo′转动时有感应电流产生,当线框绕轴ab转动时无 感应电流产生.(填有、无)