题目内容
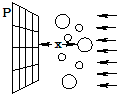 有许多大小不同的气球漂浮在空气中,如图所示,图中左边P为固定的透风网格,气球受到水平向左的恒定风力的作用,可作匀加速运动.已知风对气球的作用力与球的最大截面成正比,即F=kS(k为一常量).对气球来说空间存在一个风力场,类比于电场和重力场,请你完成以下问题.
有许多大小不同的气球漂浮在空气中,如图所示,图中左边P为固定的透风网格,气球受到水平向左的恒定风力的作用,可作匀加速运动.已知风对气球的作用力与球的最大截面成正比,即F=kS(k为一常量).对气球来说空间存在一个风力场,类比于电场和重力场,请你完成以下问题.(1)请你定义风力场的强度及表达式.
(2)由在该风力场中风力对气球做功与路径无关(气球运动时所受阻力不计),可引入风力势能和风力势的概念.若以网格P为零势能参考平面,写出风力势能Ep和风力势U的表达式.
(3)写出风力场中机械能守恒定律的表达式(对气球而言,阻力不计.气球平均密度为ρ,气球半径为r,第一状态速度为v1,位置为x1;第二状态速度为v2,位置为x2).
(4)某一气球半径为r=0.1m,在网格中1m处以v0=10m/s初速度斜向抛出,它落到网格P处的速度为多大(空气密度ρ=1.3kg/m3,比例常数k=10N/m2)?
分析:本题可以类比电场强度进行分析,风力强度类似于电场强度,与所受的分力无关,电场力所做的功等于电势能的减小量,则风力势能的减小量等于风力所做的功.
解答:解:(1)类比于电场,可定义风力场强度为风对球的作用力与球的最大截面之比,
即E=
=k,方向向左与风的方向一致.
(2)设球离零势能参考面P距离为x(x与风力方向平行),类比于重力场得:
Ep=W=kSx,
类比于电场得:U=
=kx(风力势仅取决于场的性质,与球无关).
(3)机械能守恒定律表达式为:
mv12+kSx1=
mv22+kSx2.
由于m=ρV=ρ
πr3,S=πr2,代入上式后得到:
ρrv12+kx1=
ρrv22+kx2.
这就是在该风力场中机械能守恒的普遍表达式.
(4)因为
ρrv12+kx1=
ρrv22,
所以v2=
=
=14.68m/s
答:(1)风力场强度为风对球的作用力与球的最大截面之比,E=
=k,方向向左与风的方向一致..
(2)风力势能Ep和风力势U的表达式为U=
.
(3)风力场中机械能守恒定律的表达式为
ρrv12+kx1=
ρrv22+kx2;
(4)它落到网格P处的速度为14.68m/s
即E=
| F |
| S |
(2)设球离零势能参考面P距离为x(x与风力方向平行),类比于重力场得:
Ep=W=kSx,
类比于电场得:U=
| EP |
| S |
(3)机械能守恒定律表达式为:
| 1 |
| 2 |
| 1 |
| 2 |
由于m=ρV=ρ
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
这就是在该风力场中机械能守恒的普遍表达式.
(4)因为
| 2 |
| 3 |
| 2 |
| 3 |
所以v2=
|
|
答:(1)风力场强度为风对球的作用力与球的最大截面之比,E=
| F |
| S |
(2)风力势能Ep和风力势U的表达式为U=
| EP |
| S |
(3)风力场中机械能守恒定律的表达式为
| 2 |
| 3 |
| 2 |
| 3 |
(4)它落到网格P处的速度为14.68m/s
点评:解决本题的关键采用类比的方法,风力强度类比于电场强度,风力做功与风力势能的关系类比于电场力做功与电势能的关系.

练习册系列答案
相关题目