题目内容
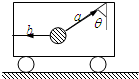 平直路上向右运动的小车内,用细绳a和水平绳b系住一个小球质量为3kg的小球,绳a与竖直方向成θ=53°角,如图所示,g 取 10m/s2求:
平直路上向右运动的小车内,用细绳a和水平绳b系住一个小球质量为3kg的小球,绳a与竖直方向成θ=53°角,如图所示,g 取 10m/s2求:(1)当小车作匀速直线运动时,两绳的拉力各为多少N?
(2)假设小车向右运动过程中加速度a从0逐渐增大,则要使b绳不松驰,其小车加速度最大不超过多少?
分析:(1)小车匀速运动时,小球所受的合力为零,分析小球受力,根据平衡条件求出两绳的拉力.
(2)当车向右的加速度大到一定程度,b绳可能松驰,取b绳恰好无拉力时研究,受力分析,根据牛顿第二定律即可求解.
(2)当车向右的加速度大到一定程度,b绳可能松驰,取b绳恰好无拉力时研究,受力分析,根据牛顿第二定律即可求解.
解答: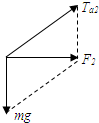
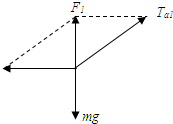 解:(1)对小球,当车匀速运动时其受力如图示,依平衡条件得:
解:(1)对小球,当车匀速运动时其受力如图示,依平衡条件得:
Ta1=
=3×
=50N
Tb1=mgtan53°=30×1.33=40N;
(2)当车向右的加速度大到一定程度,b绳可能松驰,取b绳恰好无拉力时研究,此时对小球,其受力如图
F2=mgtan53°
F2=ma
联立上述两式得a=gtan53°=10×1.33=13.3m/s2;
答:(1)当小车作匀速直线运动时,a绳的拉力为50N,b绳的拉力为40N;
(2)假设小车向右运动过程中加速度a从0逐渐增大,则要使b绳不松驰,其小车加速度最大不超过13.3m/s2.

 解:(1)对小球,当车匀速运动时其受力如图示,依平衡条件得:
解:(1)对小球,当车匀速运动时其受力如图示,依平衡条件得:Ta1=
| mg |
| cos53° |
| 10 |
| 0.6 |
Tb1=mgtan53°=30×1.33=40N;
(2)当车向右的加速度大到一定程度,b绳可能松驰,取b绳恰好无拉力时研究,此时对小球,其受力如图
F2=mgtan53°
F2=ma
联立上述两式得a=gtan53°=10×1.33=13.3m/s2;
答:(1)当小车作匀速直线运动时,a绳的拉力为50N,b绳的拉力为40N;
(2)假设小车向右运动过程中加速度a从0逐渐增大,则要使b绳不松驰,其小车加速度最大不超过13.3m/s2.
点评:本题第2问要注意分析绳子Ob刚好拉力为零的状态,分析隐含的临界状态是难点.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
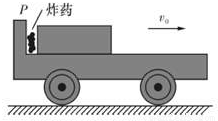
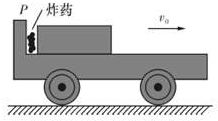 如图所示,在光滑水平的地面上,有一辆上表面光滑的正在以速度v0向右运动的小车,车上的木块一样与车一起以v0向右运动,车左端有一固定挡板P,挡板和车的质量为M=16kg,在挡板P和质量为M=9kg的木块之间有少量炸药,炸药爆炸提供给小车和木块的总机械能为E0=1800J.若要使炸药爆炸后木块的动能等于E0,在爆炸前小车的速度v0为多少?
如图所示,在光滑水平的地面上,有一辆上表面光滑的正在以速度v0向右运动的小车,车上的木块一样与车一起以v0向右运动,车左端有一固定挡板P,挡板和车的质量为M=16kg,在挡板P和质量为M=9kg的木块之间有少量炸药,炸药爆炸提供给小车和木块的总机械能为E0=1800J.若要使炸药爆炸后木块的动能等于E0,在爆炸前小车的速度v0为多少?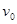 向右运动的小车,车上的木块一样与车一起以
向右运动的小车,车上的木块一样与车一起以
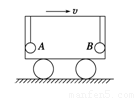
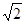 m/s向右运动的小车顶部, 两小球与小车前后竖直壁接触, 由于某种原因,小车突然停止, 此时悬线中张力之比FB∶FA为(g=10 m/s2) ( )
m/s向右运动的小车顶部, 两小球与小车前后竖直壁接触, 由于某种原因,小车突然停止, 此时悬线中张力之比FB∶FA为(g=10 m/s2) ( )