题目内容
(15分)一质量为![]() 的平顶小车,以速度
的平顶小车,以速度![]() 沿水平的光滑轨道作匀速直线运动。现将一质量为
沿水平的光滑轨道作匀速直线运动。现将一质量为![]() 的小物块无初速地放置在车顶前缘。已知物块和车顶之间的动摩擦系数为
的小物块无初速地放置在车顶前缘。已知物块和车顶之间的动摩擦系数为![]() 。
。
1. 若要求物块不会从车顶后缘掉下,则该车顶最少要多长?
2. 若车顶长度符合1问中的要求,整个过程中摩擦力共做了多少功?
解析:
1. 物块放到小车上以后,由于摩擦力的作用,当以地面为参考系时,物块将从静止开始加速运动,而小车将做减速运动,若物块到达小车顶后缘时的速度恰好等于小车此时的速度,则物块就刚好不脱落。令![]() 表示此时的速度,在这个过程中,若以物块和小车为系统,因为水平方向未受外力,所以此方向上动量守恒,即
表示此时的速度,在这个过程中,若以物块和小车为系统,因为水平方向未受外力,所以此方向上动量守恒,即
![]() (1)
(1)
从能量来看,在上述过程中,物块动能的增量等于摩擦力对物块所做的功,即
![]() (2)
(2)
其中![]() 为物块移动的距离。小车动能的增量等于摩擦力对小车所做的功,即
为物块移动的距离。小车动能的增量等于摩擦力对小车所做的功,即
![]() (3)
(3)
其中![]() 为小车移动的距离。用
为小车移动的距离。用![]() 表示车顶的最小长度,则
表示车顶的最小长度,则
![]() (4)
(4)
由以上四式,可解得
![]() (5)
(5)
即车顶的长度至少应为![]() 。
。
2.由功能关系可知,摩擦力所做的功等于系统动量的增量,即
![]() (6)
(6)
由(1)、(6)式可得
![]() (7)
(7)

 阅读快车系列答案
阅读快车系列答案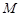 的平顶小车,以速度
的平顶小车,以速度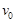 沿水平的光滑轨道作匀速直线运动。现将一质量为
沿水平的光滑轨道作匀速直线运动。现将一质量为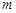 的小物块无初速地放置在车顶前缘。已知物块和车顶之间的动摩擦系数为
的小物块无初速地放置在车顶前缘。已知物块和车顶之间的动摩擦系数为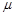 。
。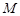 的平顶小车,以速度
的平顶小车,以速度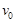 沿水平的光滑轨道作匀速直线运动。现将一质量为
沿水平的光滑轨道作匀速直线运动。现将一质量为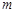 的小物块无初速地放置在车顶前缘。已知物块和车顶之间的动摩擦系数为
的小物块无初速地放置在车顶前缘。已知物块和车顶之间的动摩擦系数为 。
。