题目内容
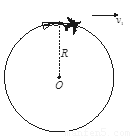
如图所示，飞行员的质量为m，重力加速度为g，他驾驶飞机在竖直平面内做翻筋斗的圆周运动，当飞机飞到最高点时速度为v1，飞行员对机座的压力恰好为零，则轨道半径R=m
| ||
| g |
m
．若飞机飞到最低点时速度为v2，飞行员对机座的压力N=
| ||
| g |
m（g+
）
| ||
| R |
m（g+
）
．
| ||
| R |
分析：当飞机飞到最高点时速度为v1，飞行员对机座的压力恰好为零，由重力提供飞行员的向心力，根据牛顿第二定律求出轨道半径．飞机飞到最低点时，机座对飞行员的支持力和重力提供飞行员的向心力，再由牛顿运动定律求解飞行员对机座的压力．
解答：解：当飞机飞到最高点时，根据牛顿第二定律得
mg=m
解得 R=
当飞机飞到最低点时，由牛顿第二定律得
FN-mg=m
解得 FN=m（g+
）
根据牛顿第三定律得知，飞行员对机座的压力N=m（g+
）．
故答案为：m
；m（g+
）．
mg=m
| ||
| R |
解得 R=
| ||
| g |
当飞机飞到最低点时，由牛顿第二定律得
FN-mg=m
| ||
| R |
解得 FN=m（g+
| ||
| R |
根据牛顿第三定律得知，飞行员对机座的压力N=m（g+
| ||
| R |
故答案为：m
| ||
| g |
| ||
| R |
点评：本题是生活中的圆周运动问题，关键是分析物体的受力情况，确定向心力的来源．
练习册系列答案
期末金牌卷系列答案
轻松课堂标准练系列答案
相关题目
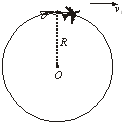如图所示，飞行员的质量为m=60kg，重力加速度为g=10m/s2，他驾驶飞机在竖直平面内做翻筋斗的圆周运动，当飞机飞到最高点时速度为v1=100m/s，飞行员对机座的压力恰好为零，则轨道半径R=
，飞行员对机座的压力恰好为零，则轨道半径R= m，若飞机飞到最低点时速度为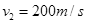
，飞行员对机座的压力N= N。
