题目内容
【题目】如图所示，一辆质量M=3kg的小车A静止在水平面上，小车上有一质量m=lkg的小物块B，将一轻质弹簧压缩并锁定，此时弹簧的弹性势能为
=6J，小物块与小车右壁距离为
=0 4m，解除锁定，小物块脱离弹簧后与小车右壁发生碰撞，碰撞过程无机械能损失，不计一切摩擦。求：
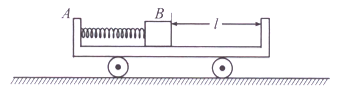
①从解除锁定到小物块与小车右壁发生第一次碰撞，小车移动的距离；
②小物块与小车右壁发生碰撞后，小物块和小车各自的速度大小和方向。
【答案】①0 1m ②小车速度方向向右为1m/s,小物块速度方向向左为3m/s
【解析】
试题分析：①设小车移动的距离为x1，小物块移动的距离为x2，从解除锁定到小物块与小车右壁碰撞过程中，水平面光滑，由小车、弹簧和小物块组成的系统动量守恒，所以有：
，
由运动关系可得：x1+x2=l，
解得：
②水平面光滑，由小车、弹簧和小物块组成的系统在从弹簧解锁到小物块脱离弹簧的过程中，满足动量守恒和能量守恒，选向右为正方向，即：mv2+Mv1=0，
解得
或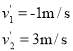
碰后小车速度方向向右为1m/s,小物块速度方向向左为3m/s
练习册系列答案
相关题目
