题目内容
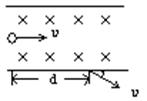
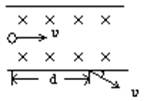
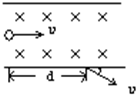 如图所示,一电子束(电子电量为e)以水平速度υ垂直于磁感应强度为B的匀强磁场中(磁场方向垂直于纸面向里),穿过磁场时,电子水平位移为d,速度方向与进入磁场时的速度方向成30°角,则:
如图所示,一电子束(电子电量为e)以水平速度υ垂直于磁感应强度为B的匀强磁场中(磁场方向垂直于纸面向里),穿过磁场时,电子水平位移为d,速度方向与进入磁场时的速度方向成30°角,则:| 2dBe |
| v |
| πd |
| 3v |
(1)电子的质量是多少?
(2)穿过磁场的时间是多少?
分析:(1)电子进入磁场中做匀速圆周运动,洛伦兹力充当向心力,画出轨迹,根据几何知识可知:电子轨迹的圆心角等于速度的偏向角,得到圆心角,即可由几何知识求出轨迹半径,由牛顿第二定律和向心力公式求出电子的质量;
(2)根据圆心角θ与时间的关系式t=
T,T=
,即可求出时间.
(2)根据圆心角θ与时间的关系式t=
| θ |
| 2π |
| 2πr |
| v |
解答:解:(1)电子进入磁场中做匀速圆周运动,画出轨迹如图. 根据几何知识可知:电子轨迹的圆心角等于速度的偏向角,可知,圆心角θ=30°,且有
根据几何知识可知:电子轨迹的圆心角等于速度的偏向角,可知,圆心角θ=30°,且有
轨迹半径r=
=2d
由evB=m
得,m=
=
(2)电子运动的周期为T=
=
=
电子穿过磁场的时间是t=
T=
T=
答:(1)电子的质量是
.
(2)穿过磁场的时间是
.
 根据几何知识可知:电子轨迹的圆心角等于速度的偏向角,可知,圆心角θ=30°,且有
根据几何知识可知:电子轨迹的圆心角等于速度的偏向角,可知,圆心角θ=30°,且有轨迹半径r=
| d |
| sinθ |
由evB=m
| v2 |
| r |
| eBr |
| v |
| 2dBe |
| v |
(2)电子运动的周期为T=
| 2πr |
| v |
| 2π?2d |
| v |
| 4πd |
| v |
电子穿过磁场的时间是t=
| θ |
| 2π |
| ||
| 2π |
| πd |
| 3v |
答:(1)电子的质量是
| 2dBe |
| v |
(2)穿过磁场的时间是
| πd |
| 3v |
点评:本题画出电子的运动轨迹,根据几何知识求解半径,确定圆心角是关键.

练习册系列答案
相关题目
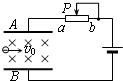 如图所示,一电子束垂直于电场线与磁感线方向入射后偏向A极板,为了使电子束沿射入方向做直线运动,可采用的方法是( )
如图所示,一电子束垂直于电场线与磁感线方向入射后偏向A极板,为了使电子束沿射入方向做直线运动,可采用的方法是( )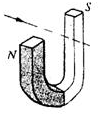 如图所示,一电子束沿图中箭头所示方向通过两磁极间时,其偏转方向为( )
如图所示,一电子束沿图中箭头所示方向通过两磁极间时,其偏转方向为( )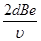 ;
;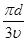 。
。