题目内容
11．
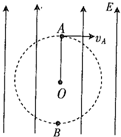如图所示，在大小为E，方向竖直向上的匀强电场中，长为L的轻绳一端固定在O点，另一端拴一个带电荷量+q的小球，已知qE=3mg，要使球能在竖直平面内做完整的圆周运动，球在A点的最小速度应为多大？
分析 根据对B点受力分析，结合牛顿第二定律，求解B点速度，再由动能定理，结合合力做功，即可求解最小速度．
解答 解：由题意可知，对小球在B点时受力分析，如图所示，
当绳子的拉力0时，小球所达到的速度最小，
由圆周运动的特点，可知，2mg=m$\frac{{v}_{B}^{2}}{R}$；
代入数据，解得，小球在B点的最小速度为：vB=$\sqrt{2gL}$；
在由B到A过程中，运用动能定理，可知，
$\frac{1}{2}$mv2min-$\frac{1}{2}$mvB2=qE•2L-mg•2L
代入数据，解得：vA=$\sqrt{10gL}$；
因此A点的小球最小速度为vA=$\sqrt{10gL}$；
答：小球在最高点A的最小速度为 $\sqrt{10gL}$
点评 本题考查带电粒子在带电场中的运动，注意明确动能定理以及向心力公式的应用，注意明确拉力为零时小球的速度最小．
练习册系列答案
云南师大附小一线名师提优作业系列答案
相关题目
1．
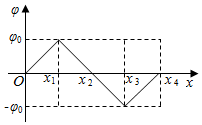在光滑的水平面内有一沿x轴的静电场，其电势φ随x坐标值的变化图线如图所示（图中φ0，-φ0，x1，x2，x3，x4均已知）．有一质量为m，带电量为q的带正电小球（可视为质点）从O点以初速度v0沿x轴正向运到点x4．下列叙述正确的是（ ）
在光滑的水平面内有一沿x轴的静电场，其电势φ随x坐标值的变化图线如图所示（图中φ0，-φ0，x1，x2，x3，x4均已知）．有一质量为m，带电量为q的带正电小球（可视为质点）从O点以初速度v0沿x轴正向运到点x4．下列叙述正确的是（ ）| A． | 带电小球在O～x1间加速，在 x1～x2 间减速 | |
| B． | 带电小球在x1～x2间减速，在 x2～x3间加速 | |
| C． | 初速度v0应满足v0≥$\sqrt{\frac{2q{φ}_{0}}{m}}$ | |
| D． | 若v0=$\sqrt{\frac{2q{φ}_{0}}{m}}$，带电小球在运动过程中的最大速度为 vm=2$\sqrt{\frac{q{φ}_{0}}{m}}$ |
2．
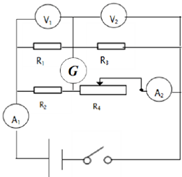如图所示，A1、A2是理想电流表，V1、V2是理想电压表，电阻R1、R2、R3均为定值电阻，R4为滑动变阻器，G为灵敏电流计，不计内阻．当滑动变阻器R4的滑片向左移动一小段距离时，灵敏电流计的读数为零，下列说法正确的是（ ）
如图所示，A1、A2是理想电流表，V1、V2是理想电压表，电阻R1、R2、R3均为定值电阻，R4为滑动变阻器，G为灵敏电流计，不计内阻．当滑动变阻器R4的滑片向左移动一小段距离时，灵敏电流计的读数为零，下列说法正确的是（ ）| A． | 滑动变阻器R4的滑片移动之前，$\frac{{R}_{1}}{{R}_{2}}＞\frac{{R}_{3}}{{R}_{4}}$ | |
| B． | 电表A1、A2示数均变大 | |
| C． | 电表V1、V2示数均变小 | |
| D． | 电源的效率变小 |
19．
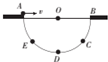如图所示，有一半球形容器，其竖直截面为半圆．AB为沿水平方向的直径，D是圆周的最低点，E是AD间某一点，C与E在相同的高度．一个可视为质点的小球从A点以速度v0水平抛出，恰好落在E点，若以2v0抛出，恰好落在C点，设球的半径为R，则下列判断正确的是（ ）
如图所示，有一半球形容器，其竖直截面为半圆．AB为沿水平方向的直径，D是圆周的最低点，E是AD间某一点，C与E在相同的高度．一个可视为质点的小球从A点以速度v0水平抛出，恰好落在E点，若以2v0抛出，恰好落在C点，设球的半径为R，则下列判断正确的是（ ）| A． | 初速度为$\frac{3{v}_{0}}{2}$时，小球恰好落在D点 | |
| B． | 初速度为$\frac{3{v}_{0}}{2}$时，小球将落在D点的左侧 | |
| C． | OC与竖直方向夹角的正弦值为$\frac{1}{4}$ | |
| D． | OE与竖直方向夹角的正弦值为$\frac{1}{3}$ |
6．
里约奥运会我国女排获得世界冠军，女排队员“重炮手”朱婷的某次发球如图，朱婷站在底线的中点外侧，球离开手时正好在底线中点正上空3.04m处，速度方向水平且在水平方向可以任意调整．已知每边球场的长和宽均为9m，球网高度为2.24m，不计空气阻力，重力加速度g=10m/s2，为了使球能落到对方场地，下列发球速度大小可行的是（ ）
里约奥运会我国女排获得世界冠军，女排队员“重炮手”朱婷的某次发球如图，朱婷站在底线的中点外侧，球离开手时正好在底线中点正上空3.04m处，速度方向水平且在水平方向可以任意调整．已知每边球场的长和宽均为9m，球网高度为2.24m，不计空气阻力，重力加速度g=10m/s2，为了使球能落到对方场地，下列发球速度大小可行的是（ ）| A． | 22m/s | B． | 23m/s | C． | 25m/s | D． | 28m/s |
16．
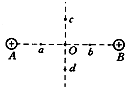如图所示，A、B为两个等量同种电荷，a、0、b在点电荷A、B的连线上，C、O、d在连线的中垂线上Oa=Ob=Oc=Od，则（ ）
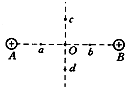如图所示，A、B为两个等量同种电荷，a、0、b在点电荷A、B的连线上，C、O、d在连线的中垂线上Oa=Ob=Oc=Od，则（ ）| A． | a、b两点的场强相同，电势也相同 | |
| B． | c、d两点的场强不相同，电势相同 | |
| C． | O点是A、B连线上电势最低的点，也是A、B连线上场强最小的点 | |
| D． | O点是中垂线cd上电势最高的点，也中垂线上场强最大的点 |
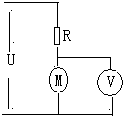有一起重机用的是直流电动机，如图所示，其内阻r=0.8Ω，线路电阻R=10Ω，电源电压U=150V，理想电压表的示数为110V，求：