题目内容
如右图所示，A、B两同学在直跑道上练习4×100 m接力，他们在奔跑时有相同的最大速度．B从静止开始全力奔跑需20 m才能达到最大速度，这一过程可看做匀变速运动，现在A持棒以最大速度向B奔来，B在接力区伺机全力奔出．若要求B接棒时速度达到最大速度的80%，则：
(1)B在接力区需跑出的距离x1为多少？
(2)B应在离A的距离x2为多少时起跑？
答案：（1）12.8m (2)19.2m
解析： (1)对B：设其加速度为a，跑出的距离为x时速度达到最大值v.
由2ax＝v2，有2ax1＝(0.8v)2，（2分）
解得x1＝0.64x＝12.8 m. （2分）
(2)设B接棒时跑出时间为t，
x1＝
t＝
t，（2分）
在t时间内，对A有xA＝vt，
解得xA＝32 m. （2分）
所以B起跑时，应距离A为Δx＝xA－x1，
得Δx＝x2＝19.2 m. （2分）
练习册系列答案
相关题目
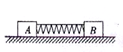如右图所示，A、B两物体质量分别为mA=5kg和mB=4kg，与水平地面之间的动摩擦因数分别为μA=0.4和μB=0.5，开始时两物体之间有一压缩的轻弹簧（不拴接），并用细线将两物体拴接在一起放在水平地面上．现将细线剪断，则两物体将被弹簧弹开，最后两物体都停在水平地面上．下列判断正确的是（ ）
