题目内容
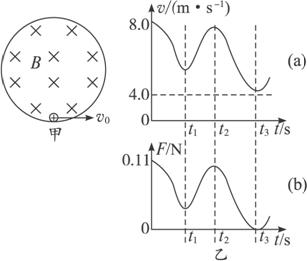
(14分)如图甲所示,在竖直平面内有一半径为R= 0.4 m的圆形绝缘轨道,匀强磁场垂直于轨道平面向里,一质量为m= 1×10-3 kg、带电荷量为q= +3×10-2 C的小球,可在内壁滚动.开始时,在最低点处给小球一个初速度v0,使小球在竖直平面内逆时针做圆周运动,图乙(a)是小球在竖直平面内做圆周运动的速率v随时间t变化的情况,图乙(b)是小球所受轨道的弹力F随时间t变化的情况,结合图象所给数据,(取g= 10 m/s2)求:
(1)匀强磁场的磁感应强度;
(2)小球的初速度v0

【答案】
(1)B = 0.25 T
(2)v0 = 8 m/s
【解析】(1)从乙图(a)可知,小球第二次过最高点时,速度大小为4 m/s,而由乙图(b)可知,此时轨道与球间的弹力为零,故mg+qvB = 
代入数据得:B = 0.25 T
(2)从乙图(b)可知,小球第一次过最低点时,轨道与球之间弹力为F = 0.11 N,根据牛顿第二定律得:F-mg+qv0B = 
代入数据:v0 = 8 m/s

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目