题目内容
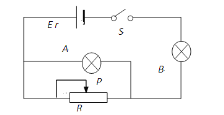
【题目】两平行金属导轨间的距离L=0.40 m,金属导轨所在的平面与水平面夹角θ=37°,在导轨所在平面内,有磁感应强度B=0.5 T、垂直于导轨所在平面的匀强磁场(方向如图所示)。金属导轨的一端接有直流电源和可变电阻R,现把一个质量m=0.05 kg 的导体棒ab 放在金属导轨上,处于静止状态,导体棒与金属导轨垂直且接触良好。已知:ab 棒与导轨间的动摩擦因数μ=0.15(可认为最大静摩擦力等于滑动摩擦力),导体棒电阻R0=2.5 Ω;直流电源的内阻r=0.5Ω,电动势E=18V,g 取10 m/s2,sin 37°=0.60,cos 37°=0.80。则:
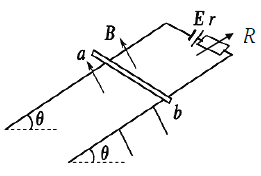
(1) 若使ab 棒所受的摩擦力恰好为零,此时通过导体棒的电流为多大?
(2) 要想ab 棒处于静止状态,则可变电阻R 取值范围为多少?
【答案】(1)I=1.5A (2) 7Ω≤R≤12Ω
【解析】(1) 若使ab 棒所受的摩擦力恰好为零,此时斜面方向上安培力和重力的分力是一对平衡力,由平衡得:
![]()
![]()
代入数值得: ![]()
(2) 若ab 棒恰不向下滑时此时导体棒受到的摩擦力沿斜面向上由平衡得:
![]()
若ab 棒恰不向上滑时此时导体棒受到的摩擦力沿斜面像下有平衡得:
![]()
依据闭合电路欧姆定律可得:
![]()
![]()
由以上各式代入数据可解得:R1=12Ω,R2=7Ω
所以R 的取值范围为:7Ω≤R≤12Ω
综上所述本题答案是:(1)I=1.5A (2) 7Ω≤R≤12Ω

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目