题目内容
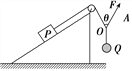
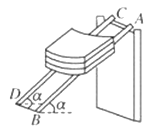
【题目】如图所示,一质量为m=0.2kg的可视为质点小物块从倾角为θ=370、高为h=0.6m的斜面顶端A处无初速自由滑下,经过斜面底端B后立刻滑上正在以v=3m/s的速度顺时针转动的水平传送带上,滑上传送带时无能量损失,已知物块与斜面和传送带之间的动摩擦因数均为μ=0.5,传送带两轮之间的距离为s=1.2m,g取10 m/s2,sin370=0.6,cos370=0.8,求:
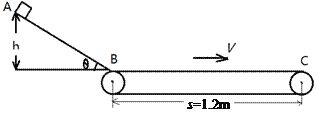
(1)物块下滑到斜面底端B处的速度大小;
(2)物体在传送带上做匀加速运动的加速度的大小和物块运动到C处的速度大小;
(3)其它条件都不变,只改变传送带的速度大小,要使物块在最短时间内到达传送带的最右端C处,传送带的速度至少为多大?
【答案】(1)2m/s(2)5m/s2;3 m/s(3)4m/s
【解析】
(1)设物块从斜面顶端A滑到底端B处的速度为vB,斜面长为s1
mgsinθ-μ mgcosθ = ma1
vB2=2 a1s1
![]()
得 vB =2m/s
(2)物块滑上传送带后,设加速度为a2,加速运动位移为s2,则
μ mg= ma2
![]()
![]()
![]()
物块滑上传送带后,先加速后匀速,物块运动到C处的速度大小为3 m/s
(3)当物块一直加速到C处时所用时间最短,则
vC2- vB2=2 a2s
传送带的最小速度为vC=4m/s

练习册系列答案
相关题目