题目内容
【题目】在如图所示的空间区域里，y轴左方有一匀强电场，场强方向跟y轴负方向成30°角，大小为E=4.0×105N/C，y轴右方有一垂直纸面的匀强磁场，有一质子以速度υ0=2.0×106m/s由x轴上A点（OA=10cm）先后两次进入磁场，第一次沿x轴正方向射入磁场，第二次沿x轴负方向射入磁场，回旋后都垂直射入电场，最后又进入磁场，已知质子质量m为1.6×10﹣27kg，不计质子重力，求：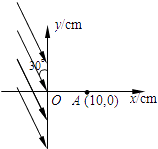
（1）匀强磁场的磁感应强度大小和方向；
（2）质子两次在磁场中运动的时间之比；
（3）质子两次在电场中运动的时间各为多少？
【答案】
（1）解：如图所示，因为质子两次均垂直进入电场，故可知质子第一、第二次由B、C两点分别进入电场，轨迹圆心分别为O1和O2．根据题意知：
所以：sin30°= 
= 
可得圆周半径：R=2×OA=0.2m
质子圆周运动中，由洛伦兹力提供圆周运动向心力，故有：
qvB= 
所以：磁感应强度：
B= 
= 
，方向垂直纸面向里．
答：匀强磁场的磁感应强度大小为0.1T，方向垂直纸面向里；
（2）解：从图中可知，第一、第二次质子在磁场中转过的角度分别为
θ1=210°和θ2=30°，因为质子在磁场中的运动时间：
所以质子两次在磁场中的运动时间为：
= 
= 
答：质子两次在磁场中运动的时间之比为7：1
（3）解：两次质子以相同的速度和夹角进入电场，所以在电场中运动的时间相同．又因为质子进入磁场后做类平抛运动，故有：
垂直电场方向质子做匀速直线运动有：S1=υ0t
质子在电场方向做初速度为0的匀加速直线运动即：
S2= 
at2= 
质子出电场时的位移夹角为30°则有：
tan30°= 
即： 
可得：t= 
= 
=1.73×10﹣7s
答：质子两次在电场中运动的时间各为=1.73×10﹣7s
【解析】带电粒子以一定的速度进入匀强磁场，仅在洛伦兹力作用下做匀速圆周运动．由入射点与出射点可确定运动圆弧半径与已知长度的关系．从而确定磁感应强度的大小与方向，再根据运动圆弧对应的圆心角结合运动周期来求出运动的时间．当从磁场射出后，恰好又垂直射入匀强电场，做类平抛运动．由平抛运动处理规律可求出电场强度的大小．
【考点精析】本题主要考查了洛伦兹力和感应电流的方向的相关知识点，需要掌握洛伦兹力始终垂直于v的方向，所以洛伦兹力一定不做功；通电导体在磁场中受力方向：跟电流方向和磁感线方向有关．（左手定则）才能正确解答此题．
