题目内容
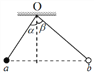
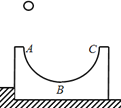
【题目】如图所示,一个质量为M,内有半径为R的半圆形轨道的长方槽体,放在光滑水平面上,左端紧靠一台阶,B为轨道最低点,其半圆形轨道的左半部AB光滑,右半部BC粗糙,一可视为质点的物体(质量为m)由离A高为R的D处自由下落,刚好由A进入轨道到达右半部分的最高点C,求此过程中两物体增加的内能为多少?(M>m)
【答案】![]()
【解析】
从D→B,轨道静止,小物体下落,机械能守恒.![]() mvB2=mg·2R ①
mvB2=mg·2R ①
从B→C水平方向上系统动量守恒mvB=(m+M)vC ②
增加的内能,等于小物体从B→C阶段系统损失机械能,根据能量守恒定律:ΔE内=-ΔE,(-ΔE表示机械能减少),
ΔE内=![]() mvB2-[
mvB2-[![]() (m+M) vC2+ mgR] ③
(m+M) vC2+ mgR] ③
解①②③式得:ΔE内=![]() mgR
mgR

练习册系列答案
相关题目