题目内容
【题目】如图是越野滑雪障碍追逐赛一段简化的赛道。某次比赛中，质量m =60 kg的运动员从 A点滑下，经过AC段赛道最低点B点时速度为20 m/s,经过BD段赛道最高点C点时的速度为10 m/s，已知B、C两点的曲率圆半径分别为R1= 10.0 m, R2 =16.0 m, A、B两点的高度差为A = 30.0 m，取g = lOm/s2。求:（赛道在同一竖直平面内）
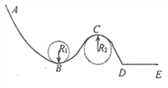
(1)从A到B，阻力对运动员做的功；
(2)运动员经过B点和C点时受到雪道的弹力。
【答案】（1）-6000J (2)225N
【解析】试题分析：对运动员从A到B运动过程应用动能定理即可求得阻力做的功；对运动员在B、C两点进行受力分析，然后根据牛顿第二定律即可求得弹力。
(1)运动员从A到B的运动过程只有重力、阻力做功，
故由动能定理可得： 
代入数据解得： 
（2）运动员在B点时，在竖直方向上应用牛顿第二定律可得
代入数据解得： 
运动员在C点时，在竖直方向上应用牛顿第二定律可得：
代入数据解得： 
练习册系列答案
初中学业考试导与练系列答案
相关题目
