题目内容
(B)如图所示的装置是某工厂用于产品分拣的传送带示意图,产品(可以忽略其形状和大小)无初速地放上水平传送带AB的最左端,当产品运动到水平传送带最右端时被挡板d挡住,分拣员在此鉴定产品质量,不合格的被取走,合格品被无初速地放在斜向传送带BC的顶端,滑至底端的传送带后再进行包装等工序.已知传送带AB、BC与产品间的动摩擦因数μ=0.5,均以v=4m/s的速度按图示方向匀速转动,水平传送带AB长L1=12m,斜向传送带BC长L2=1.64m,倾角α=37°(sin37°=0.6,cos37°=0.8,g=10m/s2),求:(1)产品刚放上水平传送带AB时,产品加速度的大小和方向;
(2)产品在水平传送带AB上运动的时间;
(3)产品在斜向传送带BC上运动的时间.

【答案】分析:(1)产品刚放上水平传送带AB时,水平方向受到向右的滑动摩擦力,由牛顿第二定律求加速度;
(2)由运动学公式求出产品加速到速度与传送带相同时所用的时间和位移,再求出匀速运动的时间,即可得到总时间;
(3)物体放在传送带上后,开始阶段,传送带的速度大于物体的速度,传送带给物体一沿斜面向下的滑动摩擦力,物体由静止开始加速下滑,当物体加速至与传送带速度相等时,由于μ<tanθ,物体在重力作用下将继续加速,此后物体的速度大于传送带的速度,传送带给物体沿传送带向上的滑动摩擦力,但合力沿传送带向下,物体继续加速下滑.由牛顿第二定律和运动学公式结合求时间.
解答:解:(1)产品刚放上水平传送带AB时,水平方向受到向右的滑动摩擦力,
由牛顿第二定律得 μmg=ma
得加速度大小为 a=5m/s2,方向水平向右.
(2)产品加速到速度传送带相同所用时间为
匀加速的位移
则匀速运动的时间
得产品在水平传送带AB上运动的时间为 t=t1+t2=3.4s
(3)第一段物体向下做匀加速直线运动,则有:mgsinθ+μmgcosθ=ma1,
则得加速度为 a1=10m/s2,
匀加速运动的时间 ,
,
位移
第二阶段,由于mgsin37°>μmgcos37°,
故物体继续向下做匀加速直线运动;
则得 mgsinθ-μmgcosθ=ma2,加速度为
第二段运动时间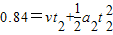 ,
,
解得 t2=0.2s
得产品在斜向传送带BC上运动的时间为t=t1+t2=0.6s
答
(1)产品刚放上水平传送带AB时,产品加速度的大小为a=5m/s2,方向水平向右;
(2)产品在水平传送带AB上运动的时间为3.4s;
(3)产品在斜向传送带BC上运动的时间是0.6s.
点评:对于物体在传送带上运动的模型,关键要分析物体的受力情况,确定出其运动情况,分段研究运动时间.
(2)由运动学公式求出产品加速到速度与传送带相同时所用的时间和位移,再求出匀速运动的时间,即可得到总时间;
(3)物体放在传送带上后,开始阶段,传送带的速度大于物体的速度,传送带给物体一沿斜面向下的滑动摩擦力,物体由静止开始加速下滑,当物体加速至与传送带速度相等时,由于μ<tanθ,物体在重力作用下将继续加速,此后物体的速度大于传送带的速度,传送带给物体沿传送带向上的滑动摩擦力,但合力沿传送带向下,物体继续加速下滑.由牛顿第二定律和运动学公式结合求时间.
解答:解:(1)产品刚放上水平传送带AB时,水平方向受到向右的滑动摩擦力,
由牛顿第二定律得 μmg=ma
得加速度大小为 a=5m/s2,方向水平向右.
(2)产品加速到速度传送带相同所用时间为

匀加速的位移

则匀速运动的时间

得产品在水平传送带AB上运动的时间为 t=t1+t2=3.4s
(3)第一段物体向下做匀加速直线运动,则有:mgsinθ+μmgcosθ=ma1,
则得加速度为 a1=10m/s2,
匀加速运动的时间
 ,
,位移

第二阶段,由于mgsin37°>μmgcos37°,
故物体继续向下做匀加速直线运动;
则得 mgsinθ-μmgcosθ=ma2,加速度为

第二段运动时间
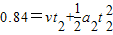 ,
,解得 t2=0.2s
得产品在斜向传送带BC上运动的时间为t=t1+t2=0.6s
答
(1)产品刚放上水平传送带AB时,产品加速度的大小为a=5m/s2,方向水平向右;
(2)产品在水平传送带AB上运动的时间为3.4s;
(3)产品在斜向传送带BC上运动的时间是0.6s.
点评:对于物体在传送带上运动的模型,关键要分析物体的受力情况,确定出其运动情况,分段研究运动时间.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目

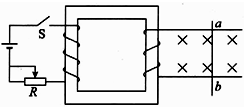 如图所示的装置中,金属杆静止在光滑的导轨上,为了让光滑金属导轨上的金属杆ab向右移动,可采取的办法有( )
如图所示的装置中,金属杆静止在光滑的导轨上,为了让光滑金属导轨上的金属杆ab向右移动,可采取的办法有( ) 一物理爱好者利用如图所示的装置研究气体压强、体积、温度三者之间的关系.导热良好的汽缸开口向下,内有理想气体,汽缸固定不动,缸内活塞可自由移动且不漏气.一温度计通过缸底小孔插入缸内,插口处密封良好,活塞下挂一个沙桶,沙桶装满沙子时活塞恰好静止.现给沙桶底部钻一个小洞,细沙缓慢漏出,外部温度恒定不变,则( )
一物理爱好者利用如图所示的装置研究气体压强、体积、温度三者之间的关系.导热良好的汽缸开口向下,内有理想气体,汽缸固定不动,缸内活塞可自由移动且不漏气.一温度计通过缸底小孔插入缸内,插口处密封良好,活塞下挂一个沙桶,沙桶装满沙子时活塞恰好静止.现给沙桶底部钻一个小洞,细沙缓慢漏出,外部温度恒定不变,则( )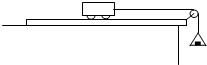 在“探究加速度与力、质量的关系”的实验中,采用如图所示的装置.本实验应用的实验方法是
在“探究加速度与力、质量的关系”的实验中,采用如图所示的装置.本实验应用的实验方法是