题目内容
在题8图所示装置中,AB是两个竖直放置的平行金属板,在两板中心处各开有一个小孔,板间距离为d,板长也为d,在两板间加上电压U后,形成水平向右的匀强电场。在B板下端(紧挨B板下端,但未接触)固定有一个点电荷Q,可以在极板外的空间形成电场。紧挨其下方有两个水平放置的金属极板CD,板间距离和板长也均为d,在两板间加上电压U后可以形成竖直向上的匀强电场。某时刻在O点沿中线![]() 由静止释放一个质量为m,带电量为q的正粒子,经过一段时间后,粒子从CD两极板的正中央进入电场,最后由CD两极板之间穿出电场。不计极板厚度及粒子的重力,假设装置产生的三个电场互不影响,静电力常量为k。求:
由静止释放一个质量为m,带电量为q的正粒子,经过一段时间后,粒子从CD两极板的正中央进入电场,最后由CD两极板之间穿出电场。不计极板厚度及粒子的重力,假设装置产生的三个电场互不影响,静电力常量为k。求:
(1)粒子经过AB两极板从B板飞出时的速度大小;
(2)在B板下端固定的点电荷Q的电性和电量;
(3)粒子从CD两极板之间飞出时的位置与释放点O之间的距离。

★★★
★★★
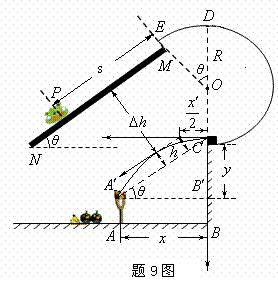
如题9图所示,弹枪![]() 离竖直墙壁BC距离
离竖直墙壁BC距离![]() ,质量
,质量![]() 的“愤怒的小鸟”从弹枪上
的“愤怒的小鸟”从弹枪上![]() 点弹出后,抛射至光滑圆弧轨道最低点C点,
点弹出后,抛射至光滑圆弧轨道最低点C点,![]() 的竖直高度差
的竖直高度差![]() 。“小鸟”在C处时,速度恰好水平地与原来静止在该处的质量为
。“小鸟”在C处时,速度恰好水平地与原来静止在该处的质量为![]() 的石块发生弹性碰撞,碰后石块沿圆弧轨道上滑,圆弧轨道半径
的石块发生弹性碰撞,碰后石块沿圆弧轨道上滑,圆弧轨道半径![]() ,石块恰好能通过圆弧最高点D,之后无碰撞地从E点离开圆弧轨道进入倾斜轨道MN(无能量损失),且斜面MN的倾角
,石块恰好能通过圆弧最高点D,之后无碰撞地从E点离开圆弧轨道进入倾斜轨道MN(无能量损失),且斜面MN的倾角![]() ,
,![]() ,石块沿斜面下滑至P点与原来藏在该处的“猪头”发生碰撞并击爆它,石块与斜面间的动摩擦因数
,石块沿斜面下滑至P点与原来藏在该处的“猪头”发生碰撞并击爆它,石块与斜面间的动摩擦因数![]() ,PE之间的距离
,PE之间的距离![]() 。已知“小鸟”、石块、“猪头”均可视为质点,重力加速度
。已知“小鸟”、石块、“猪头”均可视为质点,重力加速度![]() ,空气阻力忽略不计(
,空气阻力忽略不计(![]() ,
,![]() )。求:
)。求:
(1)石块与“猪头”碰撞时的速度大小;
(2)“小鸟”与石块碰前的速度大小;
(3)“小鸟”与石块相碰之前离斜面MN的最近距离。

解:
(1)石块恰好过圆弧最高点D,设在D点时的速度为![]()
![]() (2分)
(2分)
解得![]()
设石块在P点与“猪头”碰撞时的速度为![]() ,石块从D至P的过程,由动能定理可知
,石块从D至P的过程,由动能定理可知
![]() (2分)
(2分)
解得![]() (2分)
(2分)
(2)设石块在C点碰后的速度为![]() ,石块从C至D的过程,由动能定理可知
,石块从C至D的过程,由动能定理可知
![]() (2分)
(2分)
解得![]()
设“小鸟”与石块碰前的速度为v,碰后速度为![]() ,在碰撞过程,由动量守恒和能量守恒可知
,在碰撞过程,由动量守恒和能量守恒可知
![]() (2分)
(2分)
![]() (2分)
(2分)
联解可得 ![]() (2分)
(2分)
(3)将“小鸟”从![]() 至C的运动可逆向视为从C至
至C的运动可逆向视为从C至![]() 的平抛运动,设历时t,“小鸟”的速度与
的平抛运动,设历时t,“小鸟”的速度与![]() 连线平行,由
连线平行,由
![]()
![]()
![]() (1分)
(1分)
联解可得 ![]()
此时“小鸟”离![]() 连线的距离设为h
连线的距离设为h
![]() (1分)
(1分)
![]() (1分)
(1分)
则“小鸟”离斜面MN最近的距离为![]()
![]() (1分)
(1分)
得![]() (1分)
(1分)
 |

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案某组同学用如图所示装置,采用控制变量的方法,来研究小车质量不变的情况下,小车的加速度与小车受到力的关系。下列措施中不需要或不正确的是( )
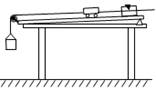
A. 平衡摩擦力的方法就是,在塑料小桶中添加砝码,使小车
在绳的拉力作用下能匀速滑动。
B. 每次改变拉小车的拉力后都需要重新平衡摩擦力
C. 实验中通过在塑料桶中增加砝码来改变小车受到的拉力
D. 实验中应先放小车,然后再开打点计时器的电源
(2)【题文】如图所示是某一次打点计时器打出的一条记录小车运动的纸带.取计数点A、B、C、D、E、F、G.纸带上两相邻计数点的时间间隔为T = 0.10s,用刻度尺测量出各相邻计数点间的距离分别为AB=1.50cm,BC=3.88 cm,CD=6.26 cm,DE=8.67 cm,EF=11.08 cm,FG=13.49cm,则小车运动的加速度大小a = m/s2,打纸带上C点时小车的瞬时速度大小v C = m/s.(结果保留二位有效数字) 。
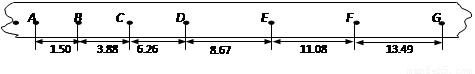
(3)【题文】某同学测得小车的加速度a和拉力F的数据如下表所示:(小车质量保持不变)
|
F/N |
0.20 |
0.30 |
0.40 |
0.50 |
0.60 |
|
a/ m/s2 |
0.30 |
0.40 |
0.48 |
0.60 |
0.72 |
①.请根据表中的数据在坐标图上作出a—F图象
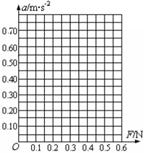
②.图象不过坐标原点的原因可能是 ,
图线的斜率的倒数的物理含义是 。


