题目内容
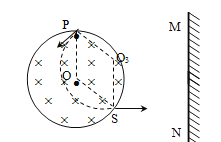
【题目】如图所示,在半径为![]() 的圆形区域内有垂直纸面向里的匀强磁场,磁感应强度B,圆形区域右侧有一竖直感光板,从圆弧顶点P以速率v0的带正电粒子平行于纸面进入磁场,已知粒子的质量为m,电量为q,粒子重力不计。
的圆形区域内有垂直纸面向里的匀强磁场,磁感应强度B,圆形区域右侧有一竖直感光板,从圆弧顶点P以速率v0的带正电粒子平行于纸面进入磁场,已知粒子的质量为m,电量为q,粒子重力不计。
(1)若磁场无边界,粒子在磁场中运动的半径r和周期T
(2)若粒子对准圆心射入,粒子在磁场中运动的时间为多少?
(3)若粒子对准圆心射入,且速率为![]() v0,求它打到感光板上时速度的垂直分量?
v0,求它打到感光板上时速度的垂直分量?
(4)若粒子以速度v0从点以任意角入射,试证明它离开磁场后均垂直打在感光板上?

【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)见解析
;(4)见解析
【解析】
(1)根据
![]()
粒子在磁场中运动的半径r
![]()
粒子在磁场中运动的周期T
![]()
(2)与磁场半径相同,故只做![]() 圆周,轨迹如图
圆周,轨迹如图
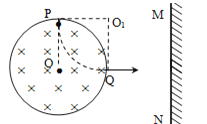
![]()
(3)速度为原来![]() 倍,半径也为原来的
倍,半径也为原来的![]() 倍,轨迹如图,
倍,轨迹如图,
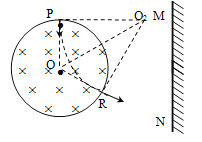
速度与墙面成60度角
![]()
(4)由(1)知,当带电粒子以![]() 射入时,粒子在磁场中的运动轨迹半径为R,设粒子射入方向与PO方向之间的夹角为
射入时,粒子在磁场中的运动轨迹半径为R,设粒子射入方向与PO方向之间的夹角为![]() ,带电粒子从区域边界S射出,带电粒子的运动轨迹如图所示
,带电粒子从区域边界S射出,带电粒子的运动轨迹如图所示
因
![]()
所以四边形![]() 为菱形,由几何关系可知,
为菱形,由几何关系可知,![]() ,在S点的速度方向与
,在S点的速度方向与![]() 垂直,即粒子打到感光板上时速度与竖直感光板的夹角为90°
垂直,即粒子打到感光板上时速度与竖直感光板的夹角为90°

练习册系列答案
相关题目