Question

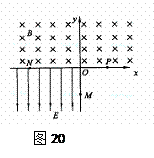
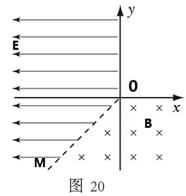
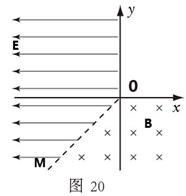
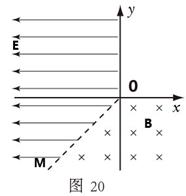
如图20所示，在纸面内建立直角坐标系xOy，以第Ⅲ象限内的直线OM（与负x轴成45°角）和正y轴为界，在x＜0的区域建立匀强电场，方向水平向左，场强大小E=0.32V/m；以直线OM和正x轴为界，在y＜0的区域建立垂直纸面向里的匀强磁场，磁感应强度B=0.1T，一不计重力的带负电粒子，从坐标原点O沿y轴负方向以v₀=2×10³m/s的初速度射入磁场，已知粒子的比荷为q/m=5×10⁶C/kg，求：

（1）粒子第一次经过磁场边界时的位置坐标

（2）粒子在磁场区域运动的总时间

（3）粒子最终离开电磁场区域时的位置坐标

Answer 1

解析：

（1）粒子带负电，从O点沿y轴负方向射入磁场，沿顺时针方向做圆周运动。

     第一次经过磁场边界上的一点（设为A点），

由得：                   …………………..2分

 m,                 …………………..1分

所以，A点的坐标为：（）。……….1分

（2）设粒子在磁场中做圆周运动的周期为T，则

，               …………………..2分

其中，                         …………………..1分

代入数据解得：，所以。..1分

（3）粒子从C点沿y轴正方向进入电场，做类平抛运动，则

       ，

，                     …………………..1分

，                           …………………..1分

代入数据解得：                ………………..1分

   …………..1分

粒子离开电磁场时的位置坐标为：（）。