题目内容
 如图所示,正方形线框在F=21N的恒力作用下向上通过水平匀强磁场,磁场宽度h=1m,磁感应强度B=1T.线框边长L=1m,质量m=0.1kg,电阻R=1Ω,线框从1处由静止开始运动,当cd边刚进入磁场时线框恰好匀速,求线框从1位置开始运动到完全穿过磁场到达2位置的过程中,恒力F做的功和线框中产生的焦耳热分别是多少?(g取10m/s2)
如图所示,正方形线框在F=21N的恒力作用下向上通过水平匀强磁场,磁场宽度h=1m,磁感应强度B=1T.线框边长L=1m,质量m=0.1kg,电阻R=1Ω,线框从1处由静止开始运动,当cd边刚进入磁场时线框恰好匀速,求线框从1位置开始运动到完全穿过磁场到达2位置的过程中,恒力F做的功和线框中产生的焦耳热分别是多少?(g取10m/s2)分析:根据平衡条件求出线框的速度大小,然后很据动能定理求出,框的cd边到磁场下边沿的距离为H,然后可以求出恒力做的功与安培力做的功,线框中产生的焦耳热等于克服安培力做的功.
解答:解:设开始时线框的cd边到磁场下边沿的距离为H,当cd刚进入磁场时作匀速运动,且h=L,所以整个线框穿过磁场时保持匀速运动,所以有:
F=F安+mg
F安=BIL=
代入数据得:v=20m/s
又(F-mg)H=
mv2,代入数据得:H=1m
所以F做的功为:WF=F(H+h+L)=63J
线框中产生的焦耳热:Q=F安(h+L)=40J
答:恒力F做的功和线框中产生的焦耳热分别是63J和40J.
F=F安+mg
F安=BIL=
| B2L2v |
| R |
代入数据得:v=20m/s
又(F-mg)H=
| 1 |
| 2 |
所以F做的功为:WF=F(H+h+L)=63J
线框中产生的焦耳热:Q=F安(h+L)=40J
答:恒力F做的功和线框中产生的焦耳热分别是63J和40J.
点评:第二问也可以由功能关系求得:Q=WF-mg(H+h+L)-
mv2=40J.
| 1 |
| 2 |

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
 (2011?唐山二模)如图所示,正方形线框的边长为L,从图示位置开始沿光滑斜面向下滑动.中途穿越垂直纸面向里,有理想边界的匀强磁场区域.磁场的宽度大于L,以i表示导线框中感应电流的强度,从线圈进入磁场开始计时,取逆时针方向为电流的正方向,在下列i-t关系图象中,可能正确的是( )
(2011?唐山二模)如图所示,正方形线框的边长为L,从图示位置开始沿光滑斜面向下滑动.中途穿越垂直纸面向里,有理想边界的匀强磁场区域.磁场的宽度大于L,以i表示导线框中感应电流的强度,从线圈进入磁场开始计时,取逆时针方向为电流的正方向,在下列i-t关系图象中,可能正确的是( ) (2004?惠州一模)如图所示,正方形线框abcd的总电阻为0.04Ω,质量为6.4g,边长为0.4m,用绝缘丝线竖直悬挂,其ab边水平,绝缘丝线的最大承受力为1N.图中两虚线之间是垂直于线框平面向里的匀强磁场,磁场上边界正好通过ad的bc有中点,磁感应强度从0.2T开始以0.1T/s的变化率均匀增大,问:
(2004?惠州一模)如图所示,正方形线框abcd的总电阻为0.04Ω,质量为6.4g,边长为0.4m,用绝缘丝线竖直悬挂,其ab边水平,绝缘丝线的最大承受力为1N.图中两虚线之间是垂直于线框平面向里的匀强磁场,磁场上边界正好通过ad的bc有中点,磁感应强度从0.2T开始以0.1T/s的变化率均匀增大,问: ,正方形线框 abcd 的总电阻为0.04Ω,质量为 6.4g,边长为0.4m,用绝缘丝线竖直悬挂,其 ab 边水平.图中两虚线之间是垂直于线框平面向里的匀强磁场,磁场上边界正好通过ac和bd的中点.磁感应强度从0.2T开始以0.1T/s的变化率均匀增大. 问:
,正方形线框 abcd 的总电阻为0.04Ω,质量为 6.4g,边长为0.4m,用绝缘丝线竖直悬挂,其 ab 边水平.图中两虚线之间是垂直于线框平面向里的匀强磁场,磁场上边界正好通过ac和bd的中点.磁感应强度从0.2T开始以0.1T/s的变化率均匀增大. 问: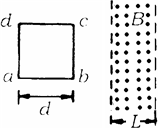 如图所示,正方形线框abcd的边长为d,向右通过宽为L的匀强磁场,且d>L,则在线框通过磁场的过程中,线框中的感应电流( )
如图所示,正方形线框abcd的边长为d,向右通过宽为L的匀强磁场,且d>L,则在线框通过磁场的过程中,线框中的感应电流( )