题目内容
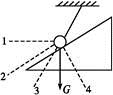
10. 如图所示,质量为2m的木板静止在光滑的水平面上,轻弹簧固定在木板左端,质量为m的小木块(视为质点)从木板右端以速度v0沿木板向左滑行,小木块撞击弹簧,使弹簧压缩到最短时,它相对木板滑行的距离为l,小木块和木板间的动摩擦因数为μ,则弹簧压缩到最短时,木板的速度是多少?弹簧的弹性势能是多少?
如图所示,质量为2m的木板静止在光滑的水平面上,轻弹簧固定在木板左端,质量为m的小木块(视为质点)从木板右端以速度v0沿木板向左滑行,小木块撞击弹簧,使弹簧压缩到最短时,它相对木板滑行的距离为l,小木块和木板间的动摩擦因数为μ,则弹簧压缩到最短时,木板的速度是多少?弹簧的弹性势能是多少?
分析 当弹簧压缩到最短时,木块和木板具有相同的速度,结合动量守恒定律和能量守恒定律求出木板的速度大小.
解答 解:当弹簧压缩到最短时,木块和木板具有相同的速度,根据动量守恒知,
mv0=3mv,
解得木块的速度为:$v=\frac{{v}_{0}}{3}$,
根据能量守恒知:$\frac{1}{2}m{{v}_{0}}^{2}-\frac{1}{2}•3m{v}^{2}={E}_{p}+μmgl$,$\frac{1}{3}m{{v}_{0}}^{2}-μmgl$
解得:Ep=$\frac{1}{3}m{{v}_{0}}^{2}-μmgl$.
答:木板的速度为$\frac{{v}_{0}}{3}$,弹簧的弹性势能是$\frac{1}{3}m{{v}_{0}}^{2}-μmgl$.
点评 本题考查了动量守恒定律和能量守恒定律的基本运用,知道当弹簧弹性势能最大时,木块和木板具有相同的速度.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
3. (多选)如图所示,地球赤道上的山丘e,近地资源卫星p和同步通信卫星q均在赤道平面上绕地心做匀速圆周运动.设e,p,q的圆周运动速率分别为v1,v2,v3,向心加速度分别为a1,a2,a3,则( )
(多选)如图所示,地球赤道上的山丘e,近地资源卫星p和同步通信卫星q均在赤道平面上绕地心做匀速圆周运动.设e,p,q的圆周运动速率分别为v1,v2,v3,向心加速度分别为a1,a2,a3,则( )
 (多选)如图所示,地球赤道上的山丘e,近地资源卫星p和同步通信卫星q均在赤道平面上绕地心做匀速圆周运动.设e,p,q的圆周运动速率分别为v1,v2,v3,向心加速度分别为a1,a2,a3,则( )
(多选)如图所示,地球赤道上的山丘e,近地资源卫星p和同步通信卫星q均在赤道平面上绕地心做匀速圆周运动.设e,p,q的圆周运动速率分别为v1,v2,v3,向心加速度分别为a1,a2,a3,则( )| A. | a1<a3<a2 | B. | v1<v3<v2 | C. | a1>a2>a3 | D. | v1>v2>v3 |
1. 如图所示,用绿光照射一光电管的阴极时产生光电效应,欲使光子从阴极逸出时的最大初动能增大,应采取的措施是( )
如图所示,用绿光照射一光电管的阴极时产生光电效应,欲使光子从阴极逸出时的最大初动能增大,应采取的措施是( )
 如图所示,用绿光照射一光电管的阴极时产生光电效应,欲使光子从阴极逸出时的最大初动能增大,应采取的措施是( )
如图所示,用绿光照射一光电管的阴极时产生光电效应,欲使光子从阴极逸出时的最大初动能增大,应采取的措施是( )| A. | 改用红光照射 | B. | 改用紫光照射 | ||
| C. | 增大绿光的强度 | D. | 增大加在光电管上的正向电压 |
18. 如图所示,A,B两点位于真空中同一条竖直的电场线上,一个带负电的微粒从A点由静止释放,微粒沿电场线下落,到达B点时速度恰好为零,下列判断正确的是( )
如图所示,A,B两点位于真空中同一条竖直的电场线上,一个带负电的微粒从A点由静止释放,微粒沿电场线下落,到达B点时速度恰好为零,下列判断正确的是( )
 如图所示,A,B两点位于真空中同一条竖直的电场线上,一个带负电的微粒从A点由静止释放,微粒沿电场线下落,到达B点时速度恰好为零,下列判断正确的是( )
如图所示,A,B两点位于真空中同一条竖直的电场线上,一个带负电的微粒从A点由静止释放,微粒沿电场线下落,到达B点时速度恰好为零,下列判断正确的是( )| A. | 微粒受到的重力可以忽略 | |
| B. | 微粒在A点的电势能比在B点的电势能小 | |
| C. | 这条电场线的方向向下 | |
| D. | 这条电场线上,电场强度处处相同 |
16. 如图甲所示,一个理想变压器原、副线圈的匝数之比n1:n2=6:1,副线圈两端接有灯泡(3V,3W),定值电阻R1=3Ω,R2=6Ω,理想二极管D,当原线圈两端接有如图乙所示的交流电源时,则有( )
如图甲所示,一个理想变压器原、副线圈的匝数之比n1:n2=6:1,副线圈两端接有灯泡(3V,3W),定值电阻R1=3Ω,R2=6Ω,理想二极管D,当原线圈两端接有如图乙所示的交流电源时,则有( )
 如图甲所示,一个理想变压器原、副线圈的匝数之比n1:n2=6:1,副线圈两端接有灯泡(3V,3W),定值电阻R1=3Ω,R2=6Ω,理想二极管D,当原线圈两端接有如图乙所示的交流电源时,则有( )
如图甲所示,一个理想变压器原、副线圈的匝数之比n1:n2=6:1,副线圈两端接有灯泡(3V,3W),定值电阻R1=3Ω,R2=6Ω,理想二极管D,当原线圈两端接有如图乙所示的交流电源时,则有( )| A. | 电阻R2两端电压的有效值为$\frac{3\sqrt{2}}{2}$V | |
| B. | 通过灯泡电流的有效值为$\frac{\sqrt{10}}{4}$A | |
| C. | 变压器副线圈两端电压的有效值为6$\sqrt{2}V$ | |
| D. | 通过灯泡电流每秒方向改变50次 |