题目内容
 (2012?上海)载流长直导线周围磁场的磁感应强度大小为B=
(2012?上海)载流长直导线周围磁场的磁感应强度大小为B=| kI | r |
(1)分别指出强度为I1、I2的电流的方向
(2)求MN分别通以强度为I1、I2的电流时,线框受到的安培力F1与F2大小之比
(3)当MN内的电流强度为I3时两细线恰好断裂,在此瞬间线圈的加速度大小为a,试求I3.
分析:(1)通过线圈处于平衡,根据共点力平衡判断安培力的方向,从而确定磁场的方向,根据右手螺旋定则确定电流的方向.
(2)通过安培力的公式分别求出线框所受的安培力,从而得出安培力之比.
(3)根据瞬间线圈的加速度,根据牛顿第二定律结合第二问的结论求出电流I3的大小,注意加速度的方向可能向上,也可能向下.
(2)通过安培力的公式分别求出线框所受的安培力,从而得出安培力之比.
(3)根据瞬间线圈的加速度,根据牛顿第二定律结合第二问的结论求出电流I3的大小,注意加速度的方向可能向上,也可能向下.
解答: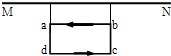 解:(1)当MN通以强度为I1的电流时,两细线内的张力均减小为T1,知此时线框所受安培力合力方向竖直向上,则ab边所受的安培力的向上,cd边所受安培力方向向下,知磁场方向垂直纸面向里,则I1方向向左.
解:(1)当MN通以强度为I1的电流时,两细线内的张力均减小为T1,知此时线框所受安培力合力方向竖直向上,则ab边所受的安培力的向上,cd边所受安培力方向向下,知磁场方向垂直纸面向里,则I1方向向左.
当MN内电流强度变为I2时,两细线内的张力均大于T0.知此时线框所受安培力合力方向竖直向下,则ab边所受的安培力的向下,cd边所受安培力方向向上,知磁场方向垂直纸面向外,则I2方向向右.
(2)当MN中通以电流I时,线圈所受安培力大小为
F1=KI1iL(
-
)
F2=KI2iL(
-
)
F1:F2=I1:I2,
(3)2T0=G
2T1+F1=G
由题意加速度向下:F3+G=
a
根据第(2)问结论:
I1:I3=F1:F3=
=
I3=
I1(方向向右)
答:(1)I1方向向左,I2方向向右.
(2)线框受到的安培力F1与F2大小之比为I1:I2,
(3)电流I3的大小为I3=
I1(方向向右)
 解:(1)当MN通以强度为I1的电流时,两细线内的张力均减小为T1,知此时线框所受安培力合力方向竖直向上,则ab边所受的安培力的向上,cd边所受安培力方向向下,知磁场方向垂直纸面向里,则I1方向向左.
解:(1)当MN通以强度为I1的电流时,两细线内的张力均减小为T1,知此时线框所受安培力合力方向竖直向上,则ab边所受的安培力的向上,cd边所受安培力方向向下,知磁场方向垂直纸面向里,则I1方向向左.当MN内电流强度变为I2时,两细线内的张力均大于T0.知此时线框所受安培力合力方向竖直向下,则ab边所受的安培力的向下,cd边所受安培力方向向上,知磁场方向垂直纸面向外,则I2方向向右.
(2)当MN中通以电流I时,线圈所受安培力大小为
F1=KI1iL(
| 1 |
| r1 |
| 1 |
| r2 |
F2=KI2iL(
| 1 |
| r1 |
| 1 |
| r2 |
F1:F2=I1:I2,
(3)2T0=G
2T1+F1=G
由题意加速度向下:F3+G=
| G |
| g |
根据第(2)问结论:
I1:I3=F1:F3=
| G-2T1 | ||
|
| (T0-T1)g |
| (a-g)T0 |
I3=
| (a-g)T0 |
| (T0-T1)g |
答:(1)I1方向向左,I2方向向右.
(2)线框受到的安培力F1与F2大小之比为I1:I2,
(3)电流I3的大小为I3=
| (a-g)T0 |
| (T0-T1)g |
点评:解决本题的关键掌握左手定则判断安培力的方向,右手螺旋定则判断电流周围磁场的方向.

练习册系列答案
相关题目