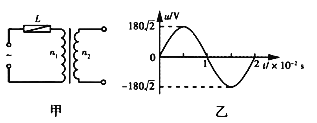
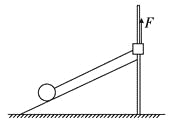
题目内容
【题目】如图所示,水平向左的匀强电场中,用长为l的绝缘轻质细绳悬挂一小球,小球质量为m,带电量为+q,将小球拉至竖直位置最低位置A点处无初速释放,小球将向左摆动,细线向左偏高竖直方向的最大角度θ=74°.
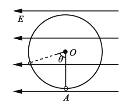
(1)求电场强度的大小E;
(2)将小球向左摆动的过程中,对细线拉力的最大值;
(3)若从A点处释放小球时,给小球一个水平向左的初速度v0,则为保证小球做完整的圆周运动,则v0的大小应满足什么条件?
【答案】(1)![]() (2)
(2)![]() mg(3)
mg(3)![]()
【解析】
试题分析:(1)由于带电小球所受电场力方向向左,电场线方向也向左,分析小球的受力情况,作出受力图如右图,根据对称性,此时必有重力与电场力的合力与角分线在同一条线上,根据平衡条件得:
qE=mgtan![]()
解得:![]()
(2)小球运动的过程中速度最大的位置,由动能定理得:qELsin![]() -mg(L-Lcos
-mg(L-Lcos![]() )=
)=![]() mv2
mv2
小球在![]() 时,由重力电场力与细线的拉力的合力提供向心力,根据牛顿第二定律得:FT-mgsin
时,由重力电场力与细线的拉力的合力提供向心力,根据牛顿第二定律得:FT-mgsin![]() -qEcos
-qEcos![]() =m
=m![]()
解得:FT=![]() mg
mg
由牛顿第三定律可知细线所受的拉力大小为![]() mg
mg
(3)当小球能完成完整的圆周运动时,需满足:![]()
根据动能定理有:-FL(1+cos![]() )=
)=![]() mv2-
mv2-![]() mv02
mv02
由上几式联立解得:![]() ;
;

【题目】为了探究质量一定时加速度与力的关系,一同学设计了如图所示的实验装置。其中M为带滑轮的小车的质量,m为砂和砂桶的质量。(滑轮质量不计)
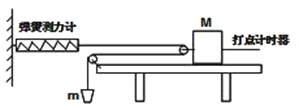
(1)实验时,一定要进行的操作是 。
A.用天平测出砂和砂桶的质量 |
B.将带滑轮的长木板右端垫高,以平衡摩擦力 |
C.小车靠近打点计时器,先接通电源,再释放小车,打出一条纸带,同时记录弹簧测力计的示数 |
D.改变砂和砂桶的质量,打出几条纸带 |
E.为减小误差,实验中一定要保证砂和砂桶的质量m远小于小车的质量M
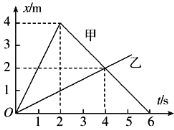
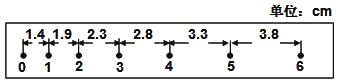
(2)该同学在实验中得到如图所示的一条纸带(两计数点间还有两个点没有画出),已知打点计时器采用的是频率为50Hz的交流电,根据纸带可求出小车的加速度为 m/s2(结果保留两位有效数字)。
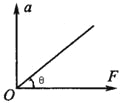
(3)以弹簧测力计的示数F为横坐标,加速度为纵坐标,画出的a—F图像是一条直线,图线与横坐标的夹角为θ,求得图线的斜率为k,则小车的质量为 。
![]()