题目内容
17.迄今发现的二百余颗太阳系外行星大多不适宜人类居住,绕恒星“Gliese581”运行的行星“G1?581c”却很值得我们期待.该行星的温度在0℃到40℃之间、质量是地球的6倍、直径是地球的1.5倍、公转周期为13天.“Gliese581”的质量是太阳质量的0.31倍.设该行星与地球均视为质量分布均匀的球体,绕其中心天体做匀速圆周运动,则( )| A. | 该行星的第一宇宙速度是地球的第一宇宙速度2倍 | |
| B. | 如果人到了该行星,其体重(重力)是地球上的2$\frac{2}{3}$倍 | |
| C. | 该行星与“Gliese581”的距离是日地距离的$\sqrt{\frac{13}{365}}$倍 | |
| D. | 行星“G1581c”绕恒星“Gliese581”运动轨道半径的三次方与周期平方之比等于地球绕太阳运动半径的三次方与周期平方之比 |
分析 根据万有引力提供向心力,列出等式表示出所要求解的第一宇宙速度和该行星与“Gliese581”的距离.根据万有引力近似等于重力,求出该行星表面与地球表面重力加速度之比,即可求出体重关系.
解答 解:A、当卫星绕行星表面附近做匀速圆周运动时的速度即为行星的第一宇宙速度,由$\frac{GMm}{{R}^{2}}=m\frac{{v}^{2}}{R}$
得v=$\sqrt{\frac{GM}{R}}$,M是行星的质量,R是行星的半径,则得该行星与地球的第一宇宙速度之比为v行:v地=$\frac{\sqrt{\frac{6GM}{1.5R}}}{\sqrt{\frac{GM}{R}}}=\frac{2}{1}$.故A正确;
B、由万有引力近似等于重力,得$\frac{GMm}{{R}^{2}}=mg$,
得行星表面的重力加速度为g=$\frac{GM}{{R}^{2}}$,则得该行星表面与地球表面重力加速度之比为g行:g地=$\frac{\frac{6GM}{(1.5R)^{2}}}{\frac{GM}{{R}^{2}}}=\frac{8}{3}$
所以如果人到了该行星,其体重是地球上的2$\frac{2}{3}$倍.故B正确;
C、根据万有引力提供向心力,列出等式$\frac{GMm}{{r}^{2}}=m\frac{4{π}^{2}r}{{T}^{2}}$
可得:r=$\root{3}{\frac{GM{T}^{2}}{4{π}^{2}}}$
行星“G1-58lc”公转周期为13个地球日.
将已知条件代入解得:行星“G1-58lc”的轨道半径与地球轨道半径r行G:r日地=$\root{3}{\frac{0.31×(13)^{2}}{36{5}^{2}}}$,故C错误;
D、根据圆周运动公式得:v=$\frac{2πr}{T}$
轨道半径r=$\root{3}{\frac{GM{T}^{2}}{4{π}^{2}}}$,所以v=2π$\root{3}{\frac{GM}{4{π}^{2}T}}$
该行星公转速率与地球公转速率之比是$\root{3}{\frac{0.31×365}{13}}$,故D错误;
故选:AB.
点评 本题行星绕恒星、卫星绕行星的类型,建立模型,根据万有引力提供向心力,万有引力近似等于重力进行求解.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案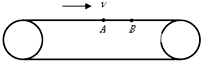 如图所示,传送带以恒定速率v运动,现将质量都是m的小物体甲、乙(视为质点)先后轻放在传送带的最左端,甲到达A处时恰好达到速率v,乙到达B处时恰好达到速率v.在甲、乙两物体在传送带上加速的过程中,下列说法正确的是( )
如图所示,传送带以恒定速率v运动,现将质量都是m的小物体甲、乙(视为质点)先后轻放在传送带的最左端,甲到达A处时恰好达到速率v,乙到达B处时恰好达到速率v.在甲、乙两物体在传送带上加速的过程中,下列说法正确的是( )| A. | 两物体的加速度相同 | |
| B. | 传送带对两物体做功相等 | |
| C. | 乙在传送带上滑行系统产生的热量与甲在传送带上滑行系统产生的热量相等 | |
| D. | 传送带克服摩擦力做的功相等 |
| A. | 牛顿通过实验精确测定了引力常量 | |
| B. | 牛顿最终给出了在科学上具有划时代意义的万有引力定律 | |
| C. | 牛顿建立的经典力学适用于宏观、高速、强引力场 | |
| D. | 牛顿建立了狭义相对论,把物理学推进到高速领域 |
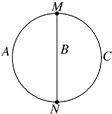 三个质点A、B、C均由N点沿不同路径运动至M点,运动轨迹如图所示,三个质点同时从N点出发,同时达到M点,下列说法正确的是( )
三个质点A、B、C均由N点沿不同路径运动至M点,运动轨迹如图所示,三个质点同时从N点出发,同时达到M点,下列说法正确的是( )| A. | 三个质点从N点到M点的平均速度相同 | |
| B. | 三个质点任意时刻的速度方向都相同 | |
| C. | 三个质点从N点出发到任意时刻的平均速度都相同 | |
| D. | 三个质点从N点到M点的位移相同,路程不同 |
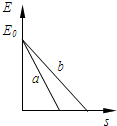 水平面上的甲、乙两物体,在某时刻动能相同,它们仅在摩擦力作用下逐渐停下来,图中,a、b分别表示甲、乙的动能E和位移s的图象,下列说法正确的是( )
水平面上的甲、乙两物体,在某时刻动能相同,它们仅在摩擦力作用下逐渐停下来,图中,a、b分别表示甲、乙的动能E和位移s的图象,下列说法正确的是( )| A. | 若甲和乙与水平面的动摩擦因数相同,则甲的质量一定比乙大 | |
| B. | 若甲和乙与水平面的动摩擦因数相同,则甲的初速度一定比乙大 | |
| C. | 若甲和乙的质量相等,则甲的运动时间一定比乙长 | |
| D. | 若甲和乙的质量相等,则甲和地面的动摩擦因数一定比乙小 |
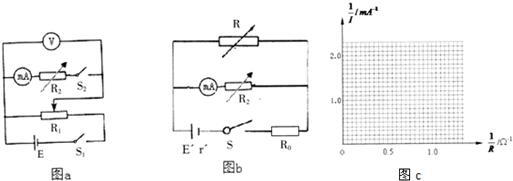
(1)改装电压表的电路如图a所示,其中
 为要改装的毫安表,V是量程为2V的标准电压表,R1为滑动变阻器,R2为电阻箱,S1、S2为开关,E为两节干电池串成的电源.请完善下列实验步骤:
为要改装的毫安表,V是量程为2V的标准电压表,R1为滑动变阻器,R2为电阻箱,S1、S2为开关,E为两节干电池串成的电源.请完善下列实验步骤:①将滑动变阻器的滑动触头调至左端(填“左”或“右”),电阻箱R2的阻值调至最大;
②断开开关S2,闭合开关S1;
③调节滑动变阻器的滑动触头,使标准电压表的读数为2.0V;
④闭合开关S2调节电阻箱R2的阻值,使毫安表指针接近满偏,此时标准电压表的读数会减小(填“增大”、“减小”或“不变”);
⑤多次重复步骤③④,直至标准电压表的读数为2.0V,同时毫安表指针满偏.
(2)图b为测电源电动势和内阻的电路图,待测电源E′的电动势约为2.0V,R0为1.0欧姆的保护电阻.闭合开关S,调整电阻箱R的阻值,读取毫安表的示数,多次改变电阻箱R的阻值,得到多组数据(如表),根据表中的数据在所给的坐标系中作出图象,由图象可知电源的电动势E′为2V,r′为1Ω.
| 外电阻$\frac{1}{R}$(Ω-1) | 电流$\frac{1}{I}$(mA-1) |
| 1.00 | 1.50 |
| 0.50 | 1.00 |
| 0.25 | 0.75 |
| 0.17 | 0.67 |
| 0.13 | 0.62 |
| A. | 小石块被竖直向上抛出后在空中运动的过程 | |
| B. | 木箱沿粗糙斜面匀速下滑的过程 | |
| C. | 人乘电梯匀速上升的过程 | |
| D. | 子弹射穿木块的过程 |
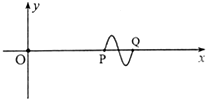 O、P、Q是x轴上的三点,OP=6m,OQ=8m.t=0时刻位于O点的振源完成一次全振动,发出一个振幅为0.4m的完整波,t=0.4s时刻,x轴上的波形如图所示.t=1.0s时刻,位于O点的振源又完成一次全振动,发出另一个与第一列波起振方向相同、振幅相同、频率不同的完整波,t=1.9s时刻,P点刚好在x轴上方最高点,则以下说法正确的是( )
O、P、Q是x轴上的三点,OP=6m,OQ=8m.t=0时刻位于O点的振源完成一次全振动,发出一个振幅为0.4m的完整波,t=0.4s时刻,x轴上的波形如图所示.t=1.0s时刻,位于O点的振源又完成一次全振动,发出另一个与第一列波起振方向相同、振幅相同、频率不同的完整波,t=1.9s时刻,P点刚好在x轴上方最高点,则以下说法正确的是( )| A. | 第一列波的起振方向向上 | |
| B. | 第一列波的传播周期为0.1s | |
| C. | 两列波的传播速度相同 | |
| D. | 第二列波的传播周期为0.8s | |
| E. | 质点P在这1.9s内通过的路程为2.0m |