题目内容
如图所示，在坐标系xOy所在平面内有一半径为a的圆形区域，圆心坐标O1（a，0），圆内分布有垂直xOy平面的匀强磁场．在坐标原点O处有一个放射源，放射源开口的张角为90°，x轴为它的角平分线．带电粒子可以从放射源开口处在纸面内朝各个方向射出，其速率v、质量m、电荷量+q均相同．其中沿x轴正方向射出的粒子恰好从O1点的正上方的P点射出．不计带电粒子的重力，且不计带电粒子间的相互作用．（1）求圆形区域内磁感应强度的大小和方向；
（2）a．判断沿什么方向射入磁场的带电粒子运动的时间最长，并求最长时间；
b．若在y≥a的区域内加一沿y轴负方向的匀强电场，放射源射出的所有带电粒子运动过程中将在某一点会聚，若在该点放一回收器可将放射源射出的带电粒子全部收回，分析并说明回收器所放的位置．
分析：（1）沿x轴正方向射出的粒子恰好从O1点的正上方的P点射出，可判断出偏转方向，利用左手定则可判磁场方向；找出圆心画出轨迹，利用几何关系可求出半径，再利用洛伦兹力提供向心力即可求出B；
（2）a、画出最上最下两个临界情况的轨迹，即可分析出沿与x轴45°向下射出的带电粒子在磁场中运动的时间最长，利用几何关系即可求出速度偏转角，从而即可求出时间；
b、画出任意方向射入磁场的轨迹，利用几何关系可发现，粒子均沿y轴正向射出，又在电场中先减速后反向匀加速回到射出点，再次进入磁场，再次画出轨迹，找出规律即可求解．
（2）a、画出最上最下两个临界情况的轨迹，即可分析出沿与x轴45°向下射出的带电粒子在磁场中运动的时间最长，利用几何关系即可求出速度偏转角，从而即可求出时间；
b、画出任意方向射入磁场的轨迹，利用几何关系可发现，粒子均沿y轴正向射出，又在电场中先减速后反向匀加速回到射出点，再次进入磁场，再次画出轨迹，找出规律即可求解．
解答：解：（1）沿x轴正方向射出的粒子恰好从O1点的正上方的P点射出，运动轨迹如图所示
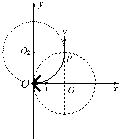
由几何关系可得R=a ①
设圆形磁场区域内的磁感应强度为B，带电粒子在磁场中所受的洛伦兹力提供向心力：qvB=m
②
①②联立得；B=
由左手定则判断磁场方向垂直于xOy平面向里
（2）经分析，沿与x轴45°向下射出的带电粒子在磁场中运动的时间最长，轨迹如图，
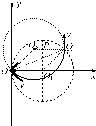
根据几何关系粒子离开磁场时速度方向沿y轴正方向，∠OO3Q=135°．
设该带电粒子在磁场中运动的时间为t，根据圆周运动周期公式得：T=
③
所以tmax=
T ④
①③④联立得：tmax=
（3）设某带电粒子从放射源射出，速度方向与x轴的夹角为α，做速度v的垂线，截取OO4=a，以O4为圆心a为半径做圆交磁场边界于M点．如图所示：
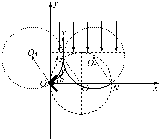
由于圆形磁场的半径与带电粒子在磁场中运动的半径均为a，故OO1MO4构成一个菱形，所以O4M与x轴平行，因此从放射源中射出的所有带电粒子均沿y轴正方向射出．带电粒子在匀强电场中做匀减速直线运动，返回磁场时的速度与离开磁场时的速度大小相等方向相反，再进入磁场做圆周运动，圆心为O5，OO4O5N构成一平行四边形，所以粒子在磁场中两次转过的圆心角之和为180°，第二次离开磁场时都经过N点．故收集器应放在N点，N点坐标为（2a，0）．
答：（1）圆形区域内磁感应强度的大小为B=
，方向垂直于xOy平面向里
（2）a、最长时间tmax=
b、（2a，0）．
由几何关系可得R=a ①
设圆形磁场区域内的磁感应强度为B，带电粒子在磁场中所受的洛伦兹力提供向心力：qvB=m
| v2 |
| R |
①②联立得；B=
| mv |
| qa |
由左手定则判断磁场方向垂直于xOy平面向里
（2）经分析，沿与x轴45°向下射出的带电粒子在磁场中运动的时间最长，轨迹如图，
根据几何关系粒子离开磁场时速度方向沿y轴正方向，∠OO3Q=135°．
设该带电粒子在磁场中运动的时间为t，根据圆周运动周期公式得：T=
| 2πR |
| v |
所以tmax=
| 135 |
| 360 |
①③④联立得：tmax=
| 3πa |
| 4v |
（3）设某带电粒子从放射源射出，速度方向与x轴的夹角为α，做速度v的垂线，截取OO4=a，以O4为圆心a为半径做圆交磁场边界于M点．如图所示：
由于圆形磁场的半径与带电粒子在磁场中运动的半径均为a，故OO1MO4构成一个菱形，所以O4M与x轴平行，因此从放射源中射出的所有带电粒子均沿y轴正方向射出．带电粒子在匀强电场中做匀减速直线运动，返回磁场时的速度与离开磁场时的速度大小相等方向相反，再进入磁场做圆周运动，圆心为O5，OO4O5N构成一平行四边形，所以粒子在磁场中两次转过的圆心角之和为180°，第二次离开磁场时都经过N点．故收集器应放在N点，N点坐标为（2a，0）．
答：（1）圆形区域内磁感应强度的大小为B=
| mv |
| qa |
（2）a、最长时间tmax=
| 3πa |
| 4v |
b、（2a，0）．
点评：解决带电粒子在磁场中的问题，关键是根据题意找出圆心，画出轨迹，一切问题可轻松解决．
练习册系列答案
相关题目
（2011?福建模拟）如图所示，在坐标系xOy中，x＜0的区域空间存在着垂直纸面向外的匀强磁场，x＞0的区域空间存在着电场强度大小E=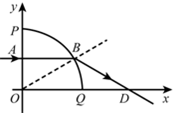
[物理--选修3-4]
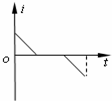
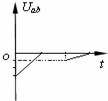
（2011?武汉模拟）如图所示，在坐标系xOy内有一半径为a的圆形区域，圆心坐标为O1（a，0），圆内分布有垂直纸面向里的匀强磁场．在直线y=a的上方和直线x=2a的左侧区域内，有一沿y轴负方向的匀强电场，场强大小为E．一质量为m、电荷量为+q（q＞0）的粒子以速度v从O点垂直于磁场方向射入，当速度方向沿x轴正方向时，粒子恰好从O1点正上方的A点射出磁场，不计粒子重力．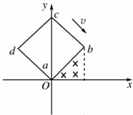
如图所示，在坐标系xOy中，有边长为L的正方形金属线框abcd，其一条对角线ac和y轴重合、顶点a位于坐标原点O处．在y轴的右侧的Ⅰ象限内有一垂直纸面向里的匀强磁场，磁场的上边界与线框的ab边刚好完全重合，下边界与x轴重合，右边界与y轴平行．t=0时刻，线圈以恒定的速度v沿垂直于磁场上边界的方向穿过磁场区域．取a→b→c→d→a的感应电流方向为正，则在线圈穿越磁场区域的过程中，感应电流i、ab间的电势差Uab随时间t变化的图线是下图中的（ ）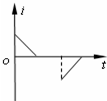
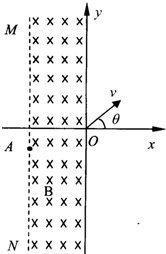如图所示，在坐标系xOy中，y轴右侧有一匀强电场；在第二、三象限内有一有界匀强磁场，其上、下边界无限远，右边界为y轴、左边界为平行于y轴的虚线，磁场的磁感应强度大小为B，方向垂直纸面向里．一带正电，电量为q、质量为m的粒子以某一速度自磁场左边界上的A点射入磁场区域，并从O点射出，粒子射出磁场的速度方向与x轴的夹角θ=45°，大小为v．粒子在磁场中的运动轨迹为纸面内的一段圆弧，且弧的半径为磁场左右边界间距的