题目内容
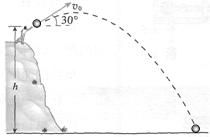
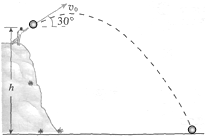
 如图所示,一人将质量为1kg的小球从h=10m高处以与水平方向成30°角斜向上方抛出,小球落地时的速度为vt=15m/s,不计空气阻力,请你用动能定理或机械能守恒定律求出小球抛出时的速度v0(g取10m/s2).
如图所示,一人将质量为1kg的小球从h=10m高处以与水平方向成30°角斜向上方抛出,小球落地时的速度为vt=15m/s,不计空气阻力,请你用动能定理或机械能守恒定律求出小球抛出时的速度v0(g取10m/s2).分析:不计空气阻力,小球抛出过程中,只有重力做功,机械能守恒,可以根据动能定理或机械能守恒定律求出小球抛出时的速度v0.
解答:解:解法一:运用动能定理.
以小球作为研究对象,对小球在空中运动过程,列动能定理有
WG=Ekt-EkO
即:mgh=
m
-
m
得 v0=
代入数据得:vt=5m/s
解法二:取地面为零势能面,由机械能守恒定律得:
m
+mgh=
m
即得v0=
代入数据得:vt=5m/s
答:小球抛出时的速度v0为5m/s.
以小球作为研究对象,对小球在空中运动过程,列动能定理有
WG=Ekt-EkO
即:mgh=
| 1 |
| 2 |
| v | 2 t |
| 1 |
| 2 |
| v | 2 0 |
得 v0=
|
代入数据得:vt=5m/s
解法二:取地面为零势能面,由机械能守恒定律得:
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 t |
即得v0=
|
代入数据得:vt=5m/s
答:小球抛出时的速度v0为5m/s.
点评:本题运用动能定理和机械能守恒两种方法研究斜抛运动,也可以采用运动的分解法求解.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 如图所示,一人坐在一辆小车上,车上还有25个质量均为m的小球,人、球与小车总质量为100m.人与车相对静止一起沿水平光滑轨道以v0运动.若人沿运动方向以相对地面5v0的速度将球一个个相继抛出.求:
如图所示,一人坐在一辆小车上,车上还有25个质量均为m的小球,人、球与小车总质量为100m.人与车相对静止一起沿水平光滑轨道以v0运动.若人沿运动方向以相对地面5v0的速度将球一个个相继抛出.求: