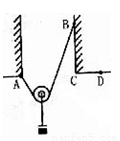
题目内容
如图所示,将一根不能伸长、柔软的轻绳两端分别系于A、B两点上,一物体用动滑轮悬挂在绳子上,达到平衡时,两段绳子间的夹角为θ1,绳子张力为F1;将绳子B端移至C点,待整个系统达到平衡时,两段绳子间的夹角为θ2,绳子张力为F2;将绳子B端移至D点,待整个系统达到平衡时,两段绳子间的夹角为θ3,绳子张力为F3,不计摩擦,则( )
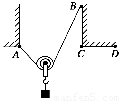
A.θ1=θ2=θ3 ??????? B.θ1=θ2<θ3
C.F1>F2>F3 ???????????? D.F1=F2<F3
【答案】
BD
【解析】由于跨过滑轮上两边绳子的拉力大小相等具有对称性,而它们的合力与物体的重力为一对平衡力,在将绳子B端移至C点的过程中,通过滑轮的移动,滑轮左边绳子的方向仍沿AO方向,滑轮右边绳子的方向仍与OB方向平行,故θ1=θ2,T1=T2;再从C点移到D点时,由于“轻绳不可伸长”,所以θ3肯定大于θ2,该过程绳子对滑轮的拉力合力与物体的重力仍然平衡,由于合力一定,而两个分力夹角增大,根据力的合成规律,两个分力一定增大,即T2<T3;根据以上分析,正确答案应该是BD.
将绳子由C端移至D点时,也可以利用正交分解来分析,以滑轮为研究对象,其受到三个力的作用而平衡,由于竖直方向上必须有2Fcos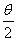 =mg,同样可以解得T3>T2.
=mg,同样可以解得T3>T2.

练习册系列答案
相关题目




 ,绳子张力为F1,将绳子B端移至C点,待整个系统达到平衡时,两段绳子间的夹角为
,绳子张力为F1,将绳子B端移至C点,待整个系统达到平衡时,两段绳子间的夹角为 ,绳子张力为F2;将绳子B端移至D点,待整个系统平衡时两段绳子间的夹角为
,绳子张力为F2;将绳子B端移至D点,待整个系统平衡时两段绳子间的夹角为 ,绳子张力为F3,不计摩擦,则
,绳子张力为F3,不计摩擦,则