��Ŀ����
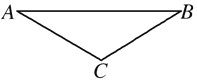
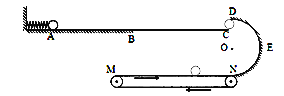
����Ŀ����ͼ��ʾ��һ����Ϊ3m�����h=0.05m��ľ��C�������ڴֲ�ˮƽ�����ϡ���ľ��C�Ͼ���һ����Ϊ2m�ĵ���С���B��B����λ�õ��Ҳ�⻬����L1=0.22m�����ֲڣ���L2=0.32m��B�������Ķ�Ħ��������1=0.9����ֱ�̶����뾶R=0.45m�Ĺ⻬![]() Բ�����������͵���ľ��C�Ҷ˵ȸ����С�����һ����Ϊm�ĵ���С���A���ӹ����ߵ��ɾ�ֹ�»�����֪C�����䶯Ħ��������2=0.25��С���A��B�ɿ�Ϊ�ʵ㣬�������ٶ�gȡ10m/s2������
Բ�����������͵���ľ��C�Ҷ˵ȸ����С�����һ����Ϊm�ĵ���С���A���ӹ����ߵ��ɾ�ֹ�»�����֪C�����䶯Ħ��������2=0.25��С���A��B�ɿ�Ϊ�ʵ㣬�������ٶ�gȡ10m/s2������
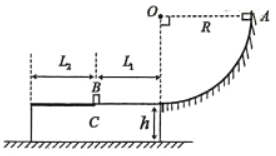
(1)A�ջ���Cʱ���ٶȴ�С��
(2)A��B����˲����ٶȴ�С��
(3)�Է����жϣ�С���A�Ƿ�Ử��ľ��C������ᣬ����С���A���˲����ľ��C�Ҷ˵�ˮƽ���롣
���𰸡���1��3m/s��2��v1=-1m/s��v2=2m/s��3���ᣬ0.108m
��������
��1��������A���ɶ��ܶ�����![]()
���![]()
��2������С���A��B��ײ��������Ϊ���������غ㶨����![]()
�������غ㶨��![]()
���v1=-1m/s��v2=2m/s
��3������С���B�����˶�����C�Ĵֲ�������C���������˶�����С���A�˶��������ң�C�ϱ����ұ߹⻬����A�����C�ұ߷ɳ�
��Aδ�ɳ�Cʱ����B��![]() ��
��![]()
��C��![]() ��a2=1m/s2
��a2=1m/s2
�辭��t1ʱ��BC���٣���ʱA��δ��C�ɳ�
![]() ��t1=0.2s��
��t1=0.2s��![]()
A��λ�ƴ�С![]() ��
��![]()
B��λ��![]() �ɵã�x2=0.22m
�ɵã�x2=0.22m
C��λ��![]() �ɵ�x3=0.02m
�ɵ�x3=0.02m
����x1+x3=0.22=L1���ʴ�ʱA�պô�C���Ҷ˷ɳ���
x2-x3=0.2<L2���ʹ���ʱBû�д�C��˷ɳ�
��BC����ʱ������Ծ�ֹһ�����
��BC��![]() ���
���![]()
��B��![]() ����BC����Ծ�ֹһ�����
����BC����Ծ�ֹһ�����
��BCһ����ٵ�0��ʱ��Ϊt3��λ��ΪXBC������
![]()
![]()
��![]()
��A���ɳ�����ƽ���˶���![]() ��
��![]()
![]() ��t2>t3��֪��BCͣ�º�A�����
��t2>t3��֪��BCͣ�º�A�����
��A���˲����ľ��C�Ҷ˵�ˮƽ����![]()