题目内容
 如图所示,粗糙的水平面与竖直平面内的光滑弯曲轨道BC在B点相接.一小物块从AB上的D点以初速v0=8m/s出发向B点滑行,DB长为12m,物块与水平面间动摩擦因数μ=0.2,
如图所示,粗糙的水平面与竖直平面内的光滑弯曲轨道BC在B点相接.一小物块从AB上的D点以初速v0=8m/s出发向B点滑行,DB长为12m,物块与水平面间动摩擦因数μ=0.2,求:(1)小物块滑到B点时的速度;
(2)小物块能沿弯曲轨道上滑到距水平面的最大高度.
分析:(1)对从D到B过程运用动能定理列式求解;
(2)物体在沿弯曲轨道上滑的过程中,只有重力对物体做功,根据动能定理列式求解.
(2)物体在沿弯曲轨道上滑的过程中,只有重力对物体做功,根据动能定理列式求解.
解答:解:(1)在到达B点前,只有滑动摩擦力f对物体做功,对物体从D到B的过程运用动能定理,设物体在B点时的速度为v,则:f?sDB=
mv2
mv02 ①
又f=μmg ②
联立以上两式解得
v=4 m/s
(2)物体在沿弯曲轨道上滑的过程中,只有重力对物体做功,设物体能够上滑的最大高度为h,根据动能定理,有:
则
mv2=mgh
解得 h=0.8m
答:(1)小物块滑到B点时的速度为4m/s;
(2)小物块能沿弯曲轨道上滑到距水平面的最大高度为0.8m.
| 1 |
| 2 |
| 1 |
| 2 |
又f=μmg ②
联立以上两式解得
v=4 m/s
(2)物体在沿弯曲轨道上滑的过程中,只有重力对物体做功,设物体能够上滑的最大高度为h,根据动能定理,有:
则
| 1 |
| 2 |
解得 h=0.8m
答:(1)小物块滑到B点时的速度为4m/s;
(2)小物块能沿弯曲轨道上滑到距水平面的最大高度为0.8m.
点评:运用动能定理解题,要合适地选择研究的过程,列表达式进行求解.有时过程选得好,可以起到事半功倍的效果.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
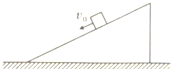 如图所示,粗糙的水平地面上有一斜劈,斜劈上一物块正在沿斜面以速度v0匀速下滑,斜劈保持静止,则地面对斜劈的摩擦力( )
如图所示,粗糙的水平地面上有一斜劈,斜劈上一物块正在沿斜面以速度v0匀速下滑,斜劈保持静止,则地面对斜劈的摩擦力( )| A、不为零,v0较大时方向向左,v0较小时方向向右 | B、不为零,方向向右 | C、不为零,方向向左 | D、等于零 |
 如图所示,粗糙的水平面上放着一个斜面体,斜面体上一个物体正在匀速下滑时,斜面体仍处于静止状态.则下列关于斜面体的说法中正确的是( )
如图所示,粗糙的水平面上放着一个斜面体,斜面体上一个物体正在匀速下滑时,斜面体仍处于静止状态.则下列关于斜面体的说法中正确的是( ) 如图所示,粗糙的水平面上放置一物体,物体在恒力F作用下做匀速直线运动,在物体发生一段位移x的过程中,求:
如图所示,粗糙的水平面上放置一物体,物体在恒力F作用下做匀速直线运动,在物体发生一段位移x的过程中,求: 如图所示,粗糙的水平地面上有三块材料完全相同的木块A、B、C,质量均为m,B、C之间用轻质细绳连接.现用一水平恒力F作用在C上,三者开始一起做匀加速运动,运动过程中把一块橡皮泥粘在某一块上面,系统仍加速运动,且始终没有相对滑动.则在粘上橡皮泥并达到稳定后,下列说法正确的是( )
如图所示,粗糙的水平地面上有三块材料完全相同的木块A、B、C,质量均为m,B、C之间用轻质细绳连接.现用一水平恒力F作用在C上,三者开始一起做匀加速运动,运动过程中把一块橡皮泥粘在某一块上面,系统仍加速运动,且始终没有相对滑动.则在粘上橡皮泥并达到稳定后,下列说法正确的是( )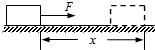 如图所示,粗糙的水平面上放置一物体,物体在恒力F作用下做匀速直线运动,在物体发生一段位移x的过程中,恒力F所做的功WF=
如图所示,粗糙的水平面上放置一物体,物体在恒力F作用下做匀速直线运动,在物体发生一段位移x的过程中,恒力F所做的功WF=