题目内容
10.一辆质量m=2.0t的小轿车,驶过半径R=90m的一段圆弧形桥面,重力加速度g=10m/s2.求:(1)若桥面为凹形,汽车以20m/s的速度通过桥面最低点时,对桥面压力是多大?
(2)若桥面为凸形,汽车以10m/s的速度通过桥面最高点时,对桥面压力是多大?
(3)汽车以多大速度通过凸形桥面顶点时,对桥面刚好没有压力?
分析 首先要确定汽车在何位置时对桥面的压力最大,汽车经过凹形桥面时,向心加速度方向向上,汽车处于超重状态;经过凸形桥面时,向心加速度方向向下,汽车处于失重状态,所以当汽车经过凹形桥面的最低点时,汽车对桥面的压力最大.
解答 解:(1)汽车通过凹形桥面最低点时,在水平方向受到牵引力F和阻力f.在竖直方向受到桥面向上的支持力N1和向下的重力G,如图(甲)所示.圆弧形轨道的圆心在汽车上方,支持力N1与重力G的合力为N1-mg,这个合力就是汽车通过桥面最低点时的向心力,即F向=N1-mg.
由向心力公式有:
N1-mg=m$\frac{{v}^{2}}{R}$,
解得桥面的支持力大小为:
N1=m$\frac{{v}^{2}}{R}$+mg=(2000×$\frac{2{0}^{2}}{90}$+2000×10)N=28900N
根据牛顿第三定律,汽车对桥面最低点的压力大小是28900N.
(2)汽车通过凸形桥面最高点时,在水平方向受到牵引力F和阻力f,在竖直方向受到竖直向下的重力G和桥面向上的支持力N2,如图(乙)所示.圆弧形轨道的圆心在汽车的下方,重力G与支持力N2 的合力为mg-N2,这个合力就是汽车通过桥面顶点时的向心力,即F向=mg-N2,由向心力公式有
mg-N2=m$\frac{{v}^{2}}{R}$,
解得桥面的支持力大小为:N2=mg-m$\frac{{v}^{2}}{R}$=(2000×10-2000×$\frac{1{0}^{2}}{90}$)=17800N
根据牛顿第三定律,汽车在桥的顶点时对桥面压力的大小为17800N.
(3)设汽车速度为vm时,通过凸形桥面顶点时对桥面压力为零.根据牛顿第三定律,这时桥面对汽车的支持力也为零,汽车在竖直方向只受到重力G作用,重力就是汽车驶过桥顶点时的向心力,由向心力公式有:
mg=m$\frac{{{v}_{m}}^{2}}{R}$,
解得:vm=$\sqrt{gR}=\sqrt{10×90}$=30m/s
汽车以30 m/s的速度通过桥面顶点时,对桥面刚好没有压力.
答:(1)若桥面为凹形,汽车以20m/s的速度通过桥面最低点时,汽车对桥面最低点的压力大小是28900N.
(2)若桥面为凸形,汽车以10m/s的速度通过桥面最高点时,对桥面压力是17800N;
(3)汽车以30m/s速度通过凸形桥面顶点时,对桥面刚好没有压力.
点评 解决本题的关键搞清向心力的来源,根据牛顿第二定律进行求解,知道汽车对桥面刚好没有压力时,由重力提供向心力,难度适中.

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案| A. | 因为v=ωr所以线速度与转动半径成正比 | |
| B. | 因为v=ωr所以线速度与角速度成正比 | |
| C. | 因为ω=$\frac{v}{r}$,所以角速度与转动半径成反比 | |
| D. | 因为ω=2πn(n为转速),所以角速度与转速成正比 |
 把一个平行玻璃板压在另一个平行玻璃板上,一端用薄片垫起,构成空气劈尖,让单色光从上方射入(如图),这时可以看到亮暗相间的条纹,下面关于条纹的说法中正确的是( )
把一个平行玻璃板压在另一个平行玻璃板上,一端用薄片垫起,构成空气劈尖,让单色光从上方射入(如图),这时可以看到亮暗相间的条纹,下面关于条纹的说法中正确的是( )| A. | 将薄片向着劈尖移动使劈角变大时,条纹变疏 | |
| B. | 将上玻璃板平行上移,条纹远离劈尖移动 | |
| C. | 将上玻璃板平行上移,条纹不动 | |
| D. | 将薄片远离劈尖移动使劈角变小时,条纹变疏 |
| A. | 若两球质量相等,碰后以某一相等速率同向而行 | |
| B. | 若两球质量相等,碰后以某一相等速率互相分开 | |
| C. | 若两球质量不同,碰后以某一相等速率互相分开 | |
| D. | 若两球质量不同,碰后以某一相等速率同向而行 |
| A. | 只有红色和绿色的干涉条纹,其它颜色的双缝干涉条纹消失 | |
| B. | 红色和绿色的干涉条纹消失,其它颜色的干涉条纹仍然存在 | |
| C. | 任何颜色的干涉条纹都不存在,但屏上仍有亮光 | |
| D. | 屏上无任何亮光 |
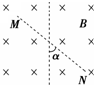 地面附近空间中存在着水平方向的匀强电场和匀强磁场,已知磁场方向垂直纸面向里,一个带电油滴沿着一条与竖直方向成α角的直线MN运动,如图所示,由此可以判断( )
地面附近空间中存在着水平方向的匀强电场和匀强磁场,已知磁场方向垂直纸面向里,一个带电油滴沿着一条与竖直方向成α角的直线MN运动,如图所示,由此可以判断( )| A. | 油滴一定做匀速运动 | |
| B. | 油滴可以做变速运动 | |
| C. | 如果油滴带正电,它是从N点运动到M点 | |
| D. | 如果油滴带正电,它是从M点运动到N点 |
 如图所示,小球在斜面顶点A处以v0=10米/秒的水平速度抛出,求小球抛出后经过多长时间离斜面的距离最大?若着地点为斜面的末端B,则斜面的长是多少?
如图所示,小球在斜面顶点A处以v0=10米/秒的水平速度抛出,求小球抛出后经过多长时间离斜面的距离最大?若着地点为斜面的末端B,则斜面的长是多少? 某学生在做实验中,忘记记下小球做平抛运动的起点位置O,若A为小球运动一段时间后的位置,试根据图中的B点(20cm,15cm)、C点(40cm,40cm),求出小球做平抛运动的起点位置O的坐标(x=-20cmy=-5cm)(g=10m/s2)
某学生在做实验中,忘记记下小球做平抛运动的起点位置O,若A为小球运动一段时间后的位置,试根据图中的B点(20cm,15cm)、C点(40cm,40cm),求出小球做平抛运动的起点位置O的坐标(x=-20cmy=-5cm)(g=10m/s2)