题目内容
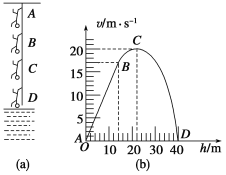
【题目】一质量为50 kg的男孩在距离河流40 m高的桥上做“蹦极跳”，原长长度为14 m的弹性绳AB一端系着他的双脚，另一端则固定在桥上的A点，如图(a) 所示，然后男孩从桥面下坠直至贴近水面的最低点D。男孩的速率v跟下坠的距离h的变化关系如图(b)所示，假定绳在整个运动过程中遵守胡克定律
(不考虑空气阻力、男孩的大小和绳的质量，g取10 m/s2)．下列说法正确的是：（ ）
A．男孩先做匀加速运动，后做变减速运动，最大位移为40m。
B．男孩的最大加速度会大于g。
C．系统储存的最大弹性势能为2×104 J。
D．弹性绳子的劲度系数为62.5N/m
【答案】BCD
【解析】
试题分析：在弹性绳伸直前，男孩只受重力作用，做匀加速直线运动，当弹性绳伸直后，由于弹性绳的弹力小于重力，男孩继续向下加速运动，只不过
中弹性绳随着绳的伸长，弹力在增大，加速度在减小，当
时，男孩的加速度为零，速度最大，之后
，所以做减速运动，
，F再增大，加速度在增大，所以男孩先做匀加速直线运动，再做变加速直线运动，后做变减速直线运动，当有最大位移时，男孩处于最低点，即40m处，A错误；从图中可知当
时速度最大，此时
，解得
，在最低点时有
，BD正确；男孩在D点时速度为零，绳子伸长量最大，绳的弹性势能最大，绳所储存的弹性势能等于男孩减少的重力势能，则
，C正确；
练习册系列答案
相关题目
