题目内容
 如图所示,长为L的绝缘细线,一端悬于O点,另一端连接带电量为一q的金属小球A,置于水平向右的匀强电场中,小球所受的电场力是其重力的
如图所示,长为L的绝缘细线,一端悬于O点,另一端连接带电量为一q的金属小球A,置于水平向右的匀强电场中,小球所受的电场力是其重力的
| ||
| 3 |
(1)求A球与B球碰撞前的速度?(小球体积可忽略不计)
(2)若(2+
| ||
| 3 |
分析:(1)小球释放后,受到向左的电场力和重力,沿着电场力和重力的合力做匀加速运动,直到绳子绷紧,由动能定理求出绳子刚绷紧时的速度.细绳突然绷紧时,小球只剩下切向速度,接着小球绕O点做圆周运动,由动能定理求出A球与B球碰撞前的速度.
(2)两球碰撞过程,机械能和动量都守恒,根据守恒关系列式,可求出碰后两球的速度.碰撞过程,两球电荷平分.B球离开桌面后运用运动的分解,根据牛顿第二定律和运动学公式求解落地时的速度大小.
(2)两球碰撞过程,机械能和动量都守恒,根据守恒关系列式,可求出碰后两球的速度.碰撞过程,两球电荷平分.B球离开桌面后运用运动的分解,根据牛顿第二定律和运动学公式求解落地时的速度大小.
解答:解:(1)如图所示,金属球A由a到b过程做匀加速直线运动,细绳与水平方向夹角为60°时突然绷紧.
由题意 qE=
mg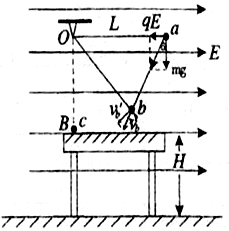
由数学知识知,α=30°
故电场力和重力的合力:F=
mg,
由动能定理得 FL=
m
-0,
求得:vb=
;
在b点细绳突然绷紧时,小球只剩下切向速度,大小为vb′=vbsin60°=
球A由b到c过程中,细绳的拉力对A球不做功,
由动能定理得 mgL(1-cos30°)+qELsin30°=
m
-
m
解之得:vc=
(2)A球与B球碰撞动量守恒和机械能不损失有:
mvc=mvc′+mvB
m
=
m
+
m
解得vB=vc=
=1 m/s(即A、B球交换速度);
A球与B球接触过程电荷量守恒有qB=-
;
B球由碰后到落地过程中竖直方向做自由落体运动:
H=
gt2,得t=
落地时,vy=gt=
=2
m/s
水平方向匀加速直线运动,
加速度为ax=
=
g
所以vx=vB+at=2m/s
则B球落地速度是v=
=4m/s
答:
(1)A球与B球碰撞前的速度是
.
(2)若(2+
)L=0.1m,H=0.6m.则B球落地时的速度大小是4m/s.
由题意 qE=
| ||
| 3 |

由数学知识知,α=30°
故电场力和重力的合力:F=
2
| ||
| 3 |
由动能定理得 FL=
| 1 |
| 2 |
| v | 2 b |
求得:vb=
|
在b点细绳突然绷紧时,小球只剩下切向速度,大小为vb′=vbsin60°=
|
球A由b到c过程中,细绳的拉力对A球不做功,
由动能定理得 mgL(1-cos30°)+qELsin30°=
| 1 |
| 2 |
| v | 2 C |
| 1 |
| 2 |
| v | ′2 b |
解之得:vc=
2gL+
|
(2)A球与B球碰撞动量守恒和机械能不损失有:
mvc=mvc′+mvB
| 1 |
| 2 |
| v | 2 c |
| 1 |
| 2 |
| v | ′2 c |
| 1 |
| 2 |
| v | 2 B |
解得vB=vc=
2gL+
|
A球与B球接触过程电荷量守恒有qB=-
| q |
| 2 |
B球由碰后到落地过程中竖直方向做自由落体运动:
H=
| 1 |
| 2 |
|
落地时,vy=gt=
| 2gH |
| 3 |
水平方向匀加速直线运动,
加速度为ax=
E?
| ||
| m |
| ||
| 6 |
所以vx=vB+at=2m/s
则B球落地速度是v=
|
答:
(1)A球与B球碰撞前的速度是
2gL+
|
(2)若(2+
| ||
| 3 |
点评:本题的物理过程较多,综合性很强,关键是分析物体的受力情况,把握每个过程遵循的物理规律,对于弹性碰撞,应根据机械能守恒和动量守恒列式,两球质量相等,会交换速度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,在场强为E的水平匀强电场中,一根长为l的绝缘杆,两端分别固定着带有电量+q和-q的小球(大小不计).现让缘绝杆绕中点O逆时针转动α角,则转动中带电小球克服电场力做功为
如图所示,在场强为E的水平匀强电场中,一根长为l的绝缘杆,两端分别固定着带有电量+q和-q的小球(大小不计).现让缘绝杆绕中点O逆时针转动α角,则转动中带电小球克服电场力做功为 如图所示,圆柱形绝热气缸(设其足够长)固定于水平面上,缸内用绝热活塞密封一定质量的理想气体,已知活塞与气缸壁的接触是光滑的,活塞的横截面积为S,大气压强为P0,电源和电热丝构成回路.可以对气体缓慢加热.开始时,电路未接通,系统处于平衡状态,封闭气体的温度为T1.现用两种方法使气缸内气体温度,均由T1缓慢升高到T2.第一次先将活塞固定,接通电路后电热丝产生的热量为Q1;第二次活塞不固定.可以缓慢自由移动,接通电路后电热丝产生的热量为Q2.
如图所示,圆柱形绝热气缸(设其足够长)固定于水平面上,缸内用绝热活塞密封一定质量的理想气体,已知活塞与气缸壁的接触是光滑的,活塞的横截面积为S,大气压强为P0,电源和电热丝构成回路.可以对气体缓慢加热.开始时,电路未接通,系统处于平衡状态,封闭气体的温度为T1.现用两种方法使气缸内气体温度,均由T1缓慢升高到T2.第一次先将活塞固定,接通电路后电热丝产生的热量为Q1;第二次活塞不固定.可以缓慢自由移动,接通电路后电热丝产生的热量为Q2.
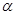 角,则转动中带电小球克服电场力做功为___________.
角,则转动中带电小球克服电场力做功为___________.