Question

如图所示，一球体绕轴O₁O₂以角速度ω旋转，A、B为球体上两点．下列说法中正确的是

[　　]

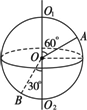
A．A、B两点具有相同的角速度

B．A、B两点具有相同的线速度

C．A、B两点具有相同的向心加速度

D．A、B两点的向心加速度方向都指向球心

Answer 1

答案：A
解析：

A、B都随球体一起绕轴O1O2旋转，转一周所用时间相等，故角速度相等，有ωA＝ωB＝ω，A做圆周运动的轨道平面与轴垂直，交点为圆心，故A的轨道半径rA＝sin60°．同理，B的轨道半径rB＝sin30°．所以两者的线速度 　　vA＝rAω＝ 　　vB＝rBω＝ 　　显然，vA＞vB 　　两者的向心加速度 　　aA＝rAω2＝ 　　aB＝rBω2＝ 　　两者的向心加速度也不相等．又两者的向心加速度指向各自的圆心，所以并不指向球心．

提示：

对于这种比较各种物理量关系的问题，通常要先找出明显的相同量或不同量(如本例中角速度相同)，然后借关系式推导出其他量的关系(例如v＝rω，a＝，a＝ω2r等)．