题目内容
15. 质量为m的物体,在汽车的牵引下由静止开始运动,当物体上升h高度时,汽车的速度为v,细绳与水平面间的夹角为θ,则下列说法中正确的是( )
质量为m的物体,在汽车的牵引下由静止开始运动,当物体上升h高度时,汽车的速度为v,细绳与水平面间的夹角为θ,则下列说法中正确的是( )| A. | 此时物体的速度大小为vsinθ | |
| B. | 此时物体的速度大小为$\frac{v}{cosθ}$ | |
| C. | 汽车对物体做的功为mgh+$\frac{{m{{(vcosθ)}^2}}}{2}$ | |
| D. | 汽车对物体做的功为mgh+$\frac{{m{{(vsinθ)}^2}}}{2}$ |
分析 小车参与两个分运动,沿绳子方向和垂直绳子方向的两个分运动,由于绳子长度一定,故物体下降的速度等于小车沿绳子方向的分速度,对物体的运动过程,根据动能定理列式求解汽车对物体做的功.
解答 解:A、小车参与两个分运动,沿绳子拉伸方向和垂直绳子方向(绕滑轮转动)的两个分运动,将小车合速度正交分解,
物体上升速度等于小车沿绳子拉伸方向的分速度为:v物=vcosθ,故AB错误;
C、对物体的运动过程,根据动能定理得:
$\frac{1}{2}{{mv}_{物}}^{2}-0=-mgh+{W}_{车}$
解得:W车=mgh+$\frac{{m{{(vcosθ)}^2}}}{2}$,故C正确,D错误.
故选:C
点评 关键要找出合运动和分运动,然后正交分解,求出分速度,能根据动能定理求解汽车对物体做的功,难度适中.

练习册系列答案
相关题目
6.如图所示的装置中,若光滑金属导轨上的金属杆ab发生向左移动,其原因可能是( )


| A. | 突然将S闭合 | B. | 突然将S断开 | ||
| C. | 闭合S后,保持电路稳定 | D. | 闭合S后,减小电阻R的阻值 |
3.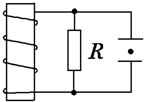 两块水平放置的金属板间的距离为d,用导线与一个n匝线圈相连,线圈电阻为r,线圈中有竖直方向的磁场,电阻R与金属板连接,如图所示,两板间有一个质量为m、电荷量-q的油滴恰好处于静止.则线圈中的磁感应强度B的变化情况和磁通量的变化率分别是( )
两块水平放置的金属板间的距离为d,用导线与一个n匝线圈相连,线圈电阻为r,线圈中有竖直方向的磁场,电阻R与金属板连接,如图所示,两板间有一个质量为m、电荷量-q的油滴恰好处于静止.则线圈中的磁感应强度B的变化情况和磁通量的变化率分别是( )
 两块水平放置的金属板间的距离为d,用导线与一个n匝线圈相连,线圈电阻为r,线圈中有竖直方向的磁场,电阻R与金属板连接,如图所示,两板间有一个质量为m、电荷量-q的油滴恰好处于静止.则线圈中的磁感应强度B的变化情况和磁通量的变化率分别是( )
两块水平放置的金属板间的距离为d,用导线与一个n匝线圈相连,线圈电阻为r,线圈中有竖直方向的磁场,电阻R与金属板连接,如图所示,两板间有一个质量为m、电荷量-q的油滴恰好处于静止.则线圈中的磁感应强度B的变化情况和磁通量的变化率分别是( )| A. | 磁感应强度B竖直向上且正增强,$\frac{△Φ}{△t}=\frac{dmg}{nq}$ | |
| B. | 磁感应强度B竖直向下且正增强,$\frac{△Φ}{△t}=\frac{dmg}{nq}$ | |
| C. | 磁感应强度B竖直向上且正减弱,$\frac{△Φ}{△t}=\frac{dmg(R+r)}{nRq}$ | |
| D. | 磁感应强度B竖直向下且正减弱,$\frac{△Φ}{△t}=\frac{dmg(R+r)}{nRq}$ |
10.2014巴西世界杯内马尔用力踢质量约为0.4kg的足球,使球由静止以20m/s的速度飞出.假定他踢球瞬间对球平均作用力是200N,球在水平方向运动了35m停止.那么他对球所做的功( )
| A. | 60 J | B. | 80 J | C. | 3000 J | D. | 7000 J |
20.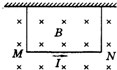 如图所示,一根通有电流I的直铜棒MN,用导线挂在磁感应强度为B的匀强磁场中,此时两根悬线处于紧张状态,下列哪些措施可使悬线中张力为零( )
如图所示,一根通有电流I的直铜棒MN,用导线挂在磁感应强度为B的匀强磁场中,此时两根悬线处于紧张状态,下列哪些措施可使悬线中张力为零( )
 如图所示,一根通有电流I的直铜棒MN,用导线挂在磁感应强度为B的匀强磁场中,此时两根悬线处于紧张状态,下列哪些措施可使悬线中张力为零( )
如图所示,一根通有电流I的直铜棒MN,用导线挂在磁感应强度为B的匀强磁场中,此时两根悬线处于紧张状态,下列哪些措施可使悬线中张力为零( )| A. | 适当减小电流 | B. | 使电流反向并适当增大 | ||
| C. | 保持电流I不变,适当增大B | D. | 使电流I反向,适当减小 |
7.利用足浴盆足浴时,人体足浴穴位会受到特定的温度刺激,改善血液循环,达到保健的目的.图甲是某品牌的足浴盆,其性能指标如下表所示.图乙是它的工作电路图,当功能转换开关接通01时,发光二极管发光,指示灯亮;开关接通02时,PTC发热元件工作加热冷水,当温度达到设定温度时,温控器自动断开电路,Rt是PTC的电阻,它的电阻值与温度的关系如图丙所示;当开关接通03时,电磁式气泵工作,产生气泡起到按摩作用,求:
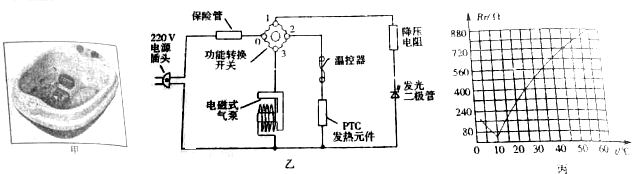
(1)电源电压为220V,当水为冷水时,PTC达到额定功率,此时它的电阻R为多少?当Rt的温度为60℃时,PTC的实际功率为多少?(温控器电阻为零)
(2)发光二极管正常发光时其两端的电压约为2V,降压电阻的阻值为20kΩ,则发光二极管的功率是多少?
| 额定电压 | 220V |
| 额定频率 | 50Hz |
| PTC额定功率 | 750W |
| 最高温度 | 60℃ |
| 水容量 | 10kg |
| 规格 | 550×400×470mm |

(1)电源电压为220V,当水为冷水时,PTC达到额定功率,此时它的电阻R为多少?当Rt的温度为60℃时,PTC的实际功率为多少?(温控器电阻为零)
(2)发光二极管正常发光时其两端的电压约为2V,降压电阻的阻值为20kΩ,则发光二极管的功率是多少?


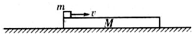 如图所示,一质量为M的木板静止在光滑的水平面上,质量为m的滑块以速度v水平滑上木板左端,滑块与木板共速时,恰好不从木板上掉落,已知m与木板的摩擦因数为μ,滑块可视为质点,求木板的长度.
如图所示,一质量为M的木板静止在光滑的水平面上,质量为m的滑块以速度v水平滑上木板左端,滑块与木板共速时,恰好不从木板上掉落,已知m与木板的摩擦因数为μ,滑块可视为质点,求木板的长度.