题目内容
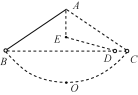
【题目】伽利略在研究运动和力的关系时,曾经考虑了一个无摩擦的理想实验:如图所示,在A点处悬挂一个质量为m的摆球,将摆球拉至B点处由静止释放,摆球将摆到与B点等高的C处;假若在A点正下方的E处钉一钉子,摆球的运动路径会发生改变,但仍能升到与开始等高的D处。若图中的摆线长为l,初始时刻摆线与竖直线之间的夹角为60°,重力加速度大小为g。求:
(1)摆球摆到最低点O时速度的大小;
(2)摆球摆到最低点O时对摆线的拉力大小;
(3)将E处的钉子下移,当钉子与A点的距离至少多大时,摆球摆下后能在竖直面内做完整的圆周运动。
【答案】(1)摆球摆到最低点![]() 时速度
时速度![]() ;(2) 摆球摆到最低点
;(2) 摆球摆到最低点![]() 时对摆线的拉力大小为
时对摆线的拉力大小为![]() ;(3)当钉子与
;(3)当钉子与![]() 的距离至少为
的距离至少为![]() 时,摆球摆下后能在竖直面内做完整的圆周运动。
时,摆球摆下后能在竖直面内做完整的圆周运动。
【解析】
(1)摆球运动过程无摩擦,摆球摆到最低点O的过程,只有重力做功,那么机械能守恒;则有:
![]()
解得:
![]() ;
;
(2)摆球摆到最低点![]() 时,由合力提供向心力,由牛顿第二定律得:
时,由合力提供向心力,由牛顿第二定律得:
![]()
可得:
![]()
由牛顿第三定律知:摆球摆到最低点![]() 时对摆线的拉力大小为
时对摆线的拉力大小为![]() 。
。
(3)设小球恰能通过最高点时,其轨道半径为![]() ,在最高点处由牛顿第二定律得:
,在最高点处由牛顿第二定律得:
![]() ;
;
从最低点到最高点由动能定理得:
![]() ;
;
解得:
![]() ;
;
所以有:
![]() ;
;
故将![]() 处的钉子下移,当钉子与
处的钉子下移,当钉子与![]() 的距离至少为
的距离至少为![]() 时,摆球摆下后能在竖直面内做完整的圆周运动。
时,摆球摆下后能在竖直面内做完整的圆周运动。

练习册系列答案
相关题目