题目内容
14.如图1所示,质量分别为如图1所示,质量分别为mA=3.0kg、mB=1.0kg的A、B两物体置于粗糙的水平面上,A、B与水平面间的动摩擦因数均为μ=0.25(A、B与水平面间的最大静摩擦力可以认为等于滑动摩擦力).一不可伸长的绳子将A、B连接,轻绳恰好处于伸直状态,且与水平方向的夹角为θ=53°,现以水平向右的力作用于物体A(sin53°=0.8,cos53°=0.6,g取10m/s2),则:
(1)若B恰好离开水平面,则B的加速度是多少?此时所施加的水平力大小F0是多少?
(2)若水平力F=32N,则轻绳的拉力T、水平面对物体B的支持力N是多少?
(3)若A、B从静止开始,所施加的水平力F由零缓慢地增加,画出水平面对物体B的摩擦力fB随F的变化图象2.
分析 (1)B离开地面时,受到地面的支持力为0,只受到重力和绳子的拉力,由此即可求出B的加速度,对整体进行受力分析,求出水平拉力;
(2)对整体进行受力分析,求出共同的加速度,然后对B进行受力分析,求出绳子的拉力和水平面对B的支持力;
(3)对A进行受力分析,求出绳子恰好拉紧的条件,然后对整体进行受力分析,求出恰好一起开始运动的条件,最后对运动的情况进行分析,综合求出水平面对物体B的摩擦力fB随F的变化规律,最后结合特定的数据作图.
解答 解:(1)B恰好距离水平面时,B与地面的作用力为0,只受到重力和绳子的拉力,设此时B的加速度为a1,对B:
水平方向:ma1=T•cosθ
竖直方向:mg=F•sinθ
联立得:${a}_{1}=7.5m/{s}^{2}$
对A、B组成的整体,由牛顿第二定律:F0-μ(mA+mB)g=(mA+mB)a1
则:F0=40N
(2)若水平力F=32N<40N,则水平面对B的支持力不是0,对A、B组成的整体:
F-μ(mA+mB)g=(mA+mB)a2
则:${a}_{2}=5.5m/{s}^{2}$
对B进行受力分析得:Tcos53°-μN=mBa2
而:Tsin53°+N=mBg
联立得:T=10N,N=2 N
(3)轻绳未绷紧时,A受到的摩擦力:fA0=μmAg=0.25×3×10=7.5N
此时B受到的摩擦力是0;
A与B没有开始运动时,A与B组成的系统受到的摩擦力:fAB=μ(mA+mB)g=0.25×(3+1)×10=10N
当:7.5≤F≤10N时,轻绳绷紧,A、B静止,则:fA=μ(mAg+T′sinθ),fB=T′cosθ,F=fA+fB
联立可得,${f}_{B}=\frac{3}{4}F-\frac{3}{4}×7.5=0.75F-5.625$ (N)
当F=10N时,fB=0.75×10-5.625=1.875N
当10N<F≤40N时,A与B一起做加速运动,则:F-μ(mA+mB)g=(mA+mB)a,T″cosθ-μ(mBg-T″sinθ)=mAa,fB=μ(mBg-T″sinθ)
联立可得:${f}_{B}=2.5-\frac{1}{16}F$
当F>40N时,B脱离地面,水平面对物体B的摩擦力是0.
所以B受到的摩擦力与拉力F之间的关系如图: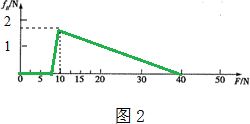
答:(1)若B恰好离开水平面,则B的加速度是7.5m/s2;此时所施加的水平力大小F0是40N;
(2)若水平力F=32N,则轻绳的拉力T是10N,水平面对物体B的支持力N是2N;
(3)如图.
点评 该题考查连接体问题,随受力的变化,B受到的力也不断发生变化,要注意对力的变化的过程中受力发生变化的临界条件的分析,明确临界条件对应的数据.

| A. | 电场强度为零的地方,电势一定为零 | |
| B. | 电势为零的地方,电场强度不一定为零 | |
| C. | 电场强度较大的地方,电势一定较高 | |
| D. | 沿着电场强度的方向,电势逐渐降低 |
| A. | 22m/s,10m/s | B. | 40m/s,14 m/s | C. | 22m/s,18 m/s | D. | 22m/s,-2m/s |
| A. | 牛顿第一定律说明,只有不受外力的物体才保持匀速直线运动或静止状态 | |
| B. | 物体运动状态发生变化则物体一定受到力的作用 | |
| C. | 惯性定律与惯性的实质是相同的 | |
| D. | 物体的运动不需要力来维持,但物体的运动速度越大时其惯性也越大 |

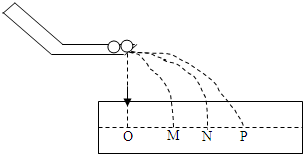 在“验证动量守恒的实验”中,实验装置如图所示.
在“验证动量守恒的实验”中,实验装置如图所示.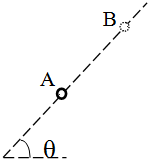 要使一带电小球沿与水平成45°的直线运动,需要外加一匀强电场,已知小球质量为m,电荷量为+Q,图中AB间距离为L.试求:
要使一带电小球沿与水平成45°的直线运动,需要外加一匀强电场,已知小球质量为m,电荷量为+Q,图中AB间距离为L.试求: 阿特伍德机是阿特伍德(G•Atwood,1746-1807)发明的一个著名力学实验装置,可以用来测定重力加速度及阐明运动定律.如图所示是阿特伍德机的示意图.已知A、B的质量为M,物体C的质量为m,B、C之间细线长以及C距地面的高度都是L,滑轮质量和摩擦不计.C落到地面后不反弹,现可测得从断开A与地面之间的细绳至C落到地面的时间为t1,从C落到地面到B与C碰撞的时间为t2,试解答下列问题:
阿特伍德机是阿特伍德(G•Atwood,1746-1807)发明的一个著名力学实验装置,可以用来测定重力加速度及阐明运动定律.如图所示是阿特伍德机的示意图.已知A、B的质量为M,物体C的质量为m,B、C之间细线长以及C距地面的高度都是L,滑轮质量和摩擦不计.C落到地面后不反弹,现可测得从断开A与地面之间的细绳至C落到地面的时间为t1,从C落到地面到B与C碰撞的时间为t2,试解答下列问题: