Question

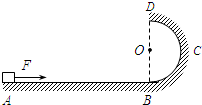如图所示，粗糙水平地面AB与半径R=0.4m的光滑半圆轨道BCD相连接，且在同一竖直平面内，O是BCD的圆心，BOD在同一竖直线上．质量m=2kg的小物体在9N的水平恒力F的作用下，从A点由静止开始做匀加速直线运动．已知AB=5m，小物块与水平地面间的动摩擦因数为μ=0.2．当小物块运动到B点时撤去力F．取重力加速度g=10m/s²．求：
（1）小物块到达B点时速度的大小；
（2）小物块运动到D点时，轨道对小物块作用力的大小；
（3）小物块离开D点落到水平地面上的点与B点之间的距离．

Answer 1

分析：（1）小物块从A到B，F做功Fx，滑动摩擦力-μmgx，根据动能定理求解小物块到达B点时速度的大小；
（2）小物块从B运动到D点过程，只有重力做功，机械能守恒，由机械能守恒定律求出物块到达D点时的速度，由牛顿第二定律求解轨道对小物块作用力的大小；
（3）小物块离开D点做平抛运动，水平方向做匀速直线运动，竖直方向做自由落体运动，由运动学公式求解落到水平地面上的点与B点之间的距离．

解答：解：（1）从A到B，根据动能定理有   
  （F-μmg）x=

1

2

m

v

2 B

得  vB=

2(F-μmg)x m

=5m/s                                   
（2）从B到D，根据机械能守恒定律有  
 

1

2

m

v

2 B

=

1

2

m

v

2 D

+mg2R
得  vD=

v 2 B -4Rg

=3m/s                                    
在D点，根据牛顿运动定律有  F+mg=m

v 2 D

R

得  F=m

v 2 D

R

-mg=25N                                       
（3）由D点到落点小物块做平抛运动，在竖直方向有  2R=

1

2

gt2
得  t=

4R g

=

4×0.4 10

=0.4s
水平面上落点与B点之间的距离为  x=v_Dt=3×0.4=1.2m     
答：（1）小物块到达B点时速度的大小是5m/s；
（2）小物块运动到D点时，轨道对小物块作用力的大小是25N；
（3）小物块离开D点落到水平地面上的点与B点之间的距离是1.2m．

点评：本题是动能定理、牛顿第二定律和平抛运动规律的综合应用，关键是确定运动过程，分析运动规律．